题目内容
3.反比例函数y=$\frac{m}{x}$与一次函数y=-x-$\frac{m}{2}$的图象在第二象限内的交点为A,过点A作AB⊥x轴,垂足为点B,△ABO的面积为2,一次函数的图象与x轴交点为C,与y轴交点为D,求这两个函数解析式及△DOC的面积.分析 根据反比例函数的图象所在的象限判断出k的符号,在由△ABO的面积求出k的值,进而可得出两个函数的解析式;根据求得的一次函数的解析式求得C、D的坐标,然后根据三角形面积公式即可求得△DOC的面积.
解答 解:∵反比例函数y=$\frac{m}{x}$的图象在二、四象限,
∴m<0,
∵S△ABO=$\frac{1}{2}$|m|=2,
∴m=-4,
∴反比例函数的解析式为:y=-$\frac{4}{x}$,
一次函数的解析式为:y=-x-$\frac{-4}{2}$,即y=-x+2;
∵一次函数的图象与x轴交点为C,与y轴交点为D,
∴C(2,0),D(0,2),
∴△DOC的面积=$\frac{1}{2}$×2×2=2.
点评 本题考查的是反比例函数与一次函数的交点问题,待定系数法求一次函数及反比例函数的解析式,能根据△ABO的面积求出m的值是解答此题的关键.

练习册系列答案
相关题目
18.在Rt△ABC中,∠C=90°,其内切圆半径为2cm,斜边AB=10cm,那么△ABC的面积是( )
| A. | 48cm2 | B. | 24cm2 | C. | 20cm2 | D. | 12cm2 |
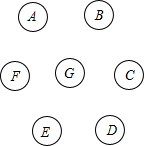 如图,一个旅游区有7个不在一条直线上的A,B,C,D,E,F,G风景点,现准备开设电车线路免费接送游客,电车线路应满足以下条件:
如图,一个旅游区有7个不在一条直线上的A,B,C,D,E,F,G风景点,现准备开设电车线路免费接送游客,电车线路应满足以下条件: