题目内容
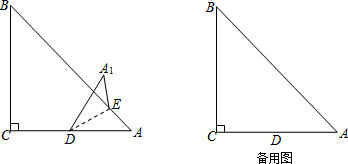
15.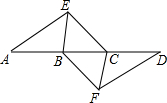 如图,点A,B,C,D在同一条直线上,点E,F分别在直线AD的两侧,且AE=DF,∠A=∠D,AB=DC.
如图,点A,B,C,D在同一条直线上,点E,F分别在直线AD的两侧,且AE=DF,∠A=∠D,AB=DC.(1)求证:四边形BFCE是平行四边形;
(2)若AD=7cm,DC=2cm,∠EBD=60°,则BE=3cm时,四边形BFCE是菱形.
分析 (1)直接利用全等三角形的判定方法得出△ABE≌△DCF(SAS),进而求出BE=FC,BE∥FC,即可得出答案;
(2)直接利用菱形的性质得出△EBC是等边三角形,进而得出答案.
解答  (1)证明:在△ABE和△DCF中,
(1)证明:在△ABE和△DCF中,
$\left\{\begin{array}{l}{AB=DC}\\{∠A=∠D}\\{AE=DF}\end{array}\right.$,
∴△ABE≌△DCF(SAS),
∴BE=FC,∠ABE=∠DCF,
∴∠EBC=∠FCB,
∴BE∥FC,
∴四边形BFCE是平行四边形;
(2)解:当四边形BFCE是菱形,
则BE=EC,
∵AD=7cm,DC=2cm,AB=DC,
∴BC=3cm,
∵∠EBD=60°,EB=EC,
∴△EBC是等边三角形,
∴BE=3cm.
故答案为:3.
点评 此题主要考查了全等三角形的判定与性质以及菱形的性质,正确掌握菱形的性质是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.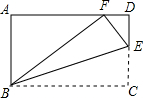 如图,在矩形ABCD中,AB=3,BC=5,点E在边CD上,连接BE,将△BCE沿BE折叠,若点C恰好落在AD边上的点F处,则CE的长为( )
如图,在矩形ABCD中,AB=3,BC=5,点E在边CD上,连接BE,将△BCE沿BE折叠,若点C恰好落在AD边上的点F处,则CE的长为( )
 如图,在矩形ABCD中,AB=3,BC=5,点E在边CD上,连接BE,将△BCE沿BE折叠,若点C恰好落在AD边上的点F处,则CE的长为( )
如图,在矩形ABCD中,AB=3,BC=5,点E在边CD上,连接BE,将△BCE沿BE折叠,若点C恰好落在AD边上的点F处,则CE的长为( )| A. | $\frac{3}{5}$ | B. | $\frac{5}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{3}$ |
3.下列各式计算正确的是( )
| A. | a3+a4=a7 | B. | (3a+b)2=9a2+b2 | C. | (-ab3)2=a2b6 | D. | a6b÷a2=a3b |
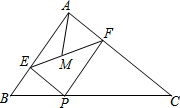 如图,在Rt△ABC中,∠BAC=90°,AB=6,AC=8,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,M为EF中点,则AM的最小值是$\frac{12}{5}$.
如图,在Rt△ABC中,∠BAC=90°,AB=6,AC=8,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,M为EF中点,则AM的最小值是$\frac{12}{5}$.
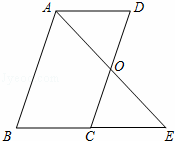 已知:?ABCD中,E是CD的中点,AE的延长线与BC的延长线相交于点F.求证:BC=CF.
已知:?ABCD中,E是CD的中点,AE的延长线与BC的延长线相交于点F.求证:BC=CF.