题目内容
7.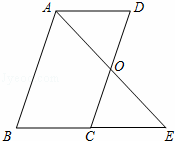 已知:?ABCD中,E是CD的中点,AE的延长线与BC的延长线相交于点F.求证:BC=CF.
已知:?ABCD中,E是CD的中点,AE的延长线与BC的延长线相交于点F.求证:BC=CF.
分析 先证明△ADE≌△FCE,得出AD=CF,再根据平行四边形的性质可知AD=BC,继而即可得出结论.
解答 证明:如图所示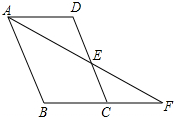
∵四边形ABCD为平行四边形,
∵AD∥BC,
∴∠ADE=∠FCE,
∵E是CD的中点,
∴DE=CE,
在△ADE和△FCE中,$\left\{\begin{array}{l}{∠ADE=∠FCE}&{\;}\\{DE=CE}&{\;}\\{∠AED=∠FEC}&{\;}\end{array}\right.$,
∴△ADE≌△FCE(ASA),
∴AD=CF,
又∵AD=BC,
∴BC=CF.
点评 本题考查平行四边形的性质及全等三角形的判定与性质;熟练掌握平行四边形的性质,证明三角形全等是解决问题的关键.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
2.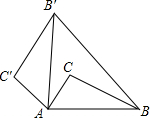 如图,将△ABC绕点A逆时针旋转80°后得到△AB′C′(点B的对应点是点B′,点C的对应点是点C′),连接BB′,若∠B′BC=20°,则∠BB′C′的大小是( )
如图,将△ABC绕点A逆时针旋转80°后得到△AB′C′(点B的对应点是点B′,点C的对应点是点C′),连接BB′,若∠B′BC=20°,则∠BB′C′的大小是( )
 如图,将△ABC绕点A逆时针旋转80°后得到△AB′C′(点B的对应点是点B′,点C的对应点是点C′),连接BB′,若∠B′BC=20°,则∠BB′C′的大小是( )
如图,将△ABC绕点A逆时针旋转80°后得到△AB′C′(点B的对应点是点B′,点C的对应点是点C′),连接BB′,若∠B′BC=20°,则∠BB′C′的大小是( )| A. | 82° | B. | 80° | C. | 78° | D. | 76° |
12. 如图是一个圆柱体的示意图,则这个圆柱体的俯视图的面积是( )
如图是一个圆柱体的示意图,则这个圆柱体的俯视图的面积是( )
 如图是一个圆柱体的示意图,则这个圆柱体的俯视图的面积是( )
如图是一个圆柱体的示意图,则这个圆柱体的俯视图的面积是( )| A. | 30 | B. | 60 | C. | 25π | D. | 60π |
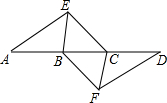 如图,点A,B,C,D在同一条直线上,点E,F分别在直线AD的两侧,且AE=DF,∠A=∠D,AB=DC.
如图,点A,B,C,D在同一条直线上,点E,F分别在直线AD的两侧,且AE=DF,∠A=∠D,AB=DC. 如图,在等边三角形ABC中,AD是高,点G为AD的中点,过G作EF∥AC交AB于点F,交CD于点E,下列说法正确的有①③④(将你认为正确选项的序号都填上).
如图,在等边三角形ABC中,AD是高,点G为AD的中点,过G作EF∥AC交AB于点F,交CD于点E,下列说法正确的有①③④(将你认为正确选项的序号都填上).