题目内容
6.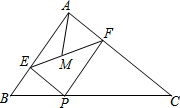 如图,在Rt△ABC中,∠BAC=90°,AB=6,AC=8,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,M为EF中点,则AM的最小值是$\frac{12}{5}$.
如图,在Rt△ABC中,∠BAC=90°,AB=6,AC=8,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,M为EF中点,则AM的最小值是$\frac{12}{5}$.
分析 根据矩形的性质就可以得出EF,AP互相平分,且EF=AP,根据垂线段最短的性质就可以得出AP⊥BC时,AP的值最小,即AM的值最小,由勾股定理求出BC,根据面积关系建立等式求出其解即可.
解答 解:∵PE⊥AB,PF⊥AC,∠BAC=90°,
∴∠EAF=∠AEP=∠AFP=90°,
∴四边形AEPF是矩形,
∴EF,AP互相平分.且EF=AP,
∴EF,AP的交点就是M点,
∵当AP的值最小时,AM的值就最小,
∴当AP⊥BC时,AP的值最小,即AM的值最小.
∵$\frac{1}{2}$AP×BC=$\frac{1}{2}$AB×AC,
∴AP×BC=AB×AC,
在Rt△ABC中,由勾股定理,得BC=$\sqrt{{6}^{2}+{8}^{2}}$=10,
∵AB=6,AC=8,
∴10AP=6×8,
∴AP=$\frac{24}{5}$
∴AM=$\frac{12}{5}$,
故答案为:$\frac{12}{5}$.
点评 本题考查了矩形的性质的运用,勾股定理的运用,三角形的面积公式的运用,垂线段最短的性质的运用,解答时求出AP的最小值是关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
11.事件A:某射击运动员射击一次,命中靶心;事件B:明天太阳从西边升起;C.13名同学中至少有两名同学的出生月份相同.3个事件的概率分别记为P(A)、P(B)、P(C),则 P(A)、P(B)、P(C)的大小关系正确的是( )
| A. | P(B)<P(A)<P(C) | B. | P(C)<P(B)<P(A) | C. | P(A)<P(B)<P(C) | D. | P(A)<P(C)<P(B) |
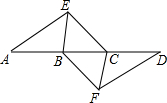 如图,点A,B,C,D在同一条直线上,点E,F分别在直线AD的两侧,且AE=DF,∠A=∠D,AB=DC.
如图,点A,B,C,D在同一条直线上,点E,F分别在直线AD的两侧,且AE=DF,∠A=∠D,AB=DC.