题目内容
5．已知菱形的边长为6，有一个内角等于60°，则它的面积为18$\sqrt{3}$．分析 作AE⊥BC于E，由三角函数求出菱形的高AE，再运用菱形面积公式=底×高计算即可．
解答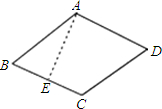 
解：作AE⊥BC于E，如图所示：
∵四边形ABCD是菱形，
∴AB=BC=6，
∴AE=AB•sinB=6×sin60°=6×$\frac{\sqrt{3}}{2}$=3$\sqrt{3}$，
∴菱形的面积S=BC•AE=6×3$\sqrt{3}$=18$\sqrt{3}$．
故答案为：18$\sqrt{3}$．
点评 本题考查了菱形的性质、三角函数、菱形的面积求法．熟练掌握菱形的性质，求出菱形的高是解决问题的关键．
练习册系列答案
相关题目
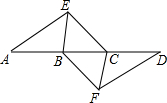如图，点A，B，C，D在同一条直线上，点E，F分别在直线AD的两侧，且AE=DF，∠A=∠D，AB=DC．
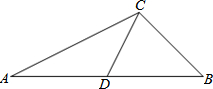如图，在△ABC中，CD是边AB上的中线，∠B是锐角，且sinB=$\frac{{\sqrt{2}}}{2}$，tanA=$\frac{1}{2}$，BC=2$\sqrt{2}$，求边AB的长和cos∠CDB的值．