题目内容
4.如图,在等腰直角△ABC中,∠ACB=90°,AC=BC=2,点D是边AC的中点,点E是斜边AB上的动点,将△ADE沿DE所在的直线折叠得到△A1DE.(1)当点A1落在边BC(含边BC的端点)上时,折痕DE的长是多少?(可在备用图上作图)
(2)连接A1B,当点E在边AB上移动时,求A1B长的最小值.
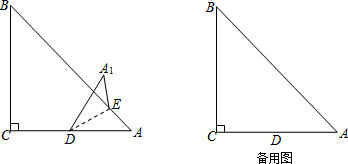
分析 (1)点A1落在边BC即点A1与点C重合,可知此时DE为△ABC的中位线,得DE=$\frac{1}{2}$BC;
(2)Rt△BCD中求出BD的长,由折叠可得A1D=AD=1,根据A1B+A1D≥BD可得A1B长的最小值.
解答 解:(1)∵点D到边BC的距离是DC=DA=1,
∴点A1落在边BC上时,点A1与点C重合,如图1所示.
此时,DE为AC的垂直平分线,即DE为△ABC的中位线,
∴DE=$\frac{1}{2}$BC=1;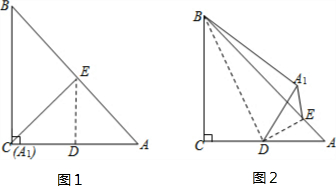
(2)连接BD,DE,
在Rt△BCD中,BD=$\sqrt{B{C}^{2}+C{D}^{2}}$=$\sqrt{5}$,
由折叠知△A1DE≌△ADE,
∴A1D=AD=1,
由A1B+A1D≥BD,得:A1B≥BD-A1D=$\sqrt{5}$-1,
∴A1B长的最小值是$\sqrt{5}$-1.
点评 本题考查了折叠的性质、勾股定理及三角形全等的判定与性质,关键是熟练掌握折叠变换的性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12. 如图是一个圆柱体的示意图,则这个圆柱体的俯视图的面积是( )
如图是一个圆柱体的示意图,则这个圆柱体的俯视图的面积是( )
 如图是一个圆柱体的示意图,则这个圆柱体的俯视图的面积是( )
如图是一个圆柱体的示意图,则这个圆柱体的俯视图的面积是( )| A. | 30 | B. | 60 | C. | 25π | D. | 60π |
9. 如图,四边形ABCD是⊙O的内接四边形,若∠C=140°,则∠BOD的度数为( )
如图,四边形ABCD是⊙O的内接四边形,若∠C=140°,则∠BOD的度数为( )
 如图,四边形ABCD是⊙O的内接四边形,若∠C=140°,则∠BOD的度数为( )
如图,四边形ABCD是⊙O的内接四边形,若∠C=140°,则∠BOD的度数为( )| A. | 70° | B. | 80° | C. | 90° | D. | 100° |
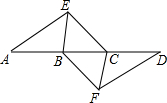 如图,点A,B,C,D在同一条直线上,点E,F分别在直线AD的两侧,且AE=DF,∠A=∠D,AB=DC.
如图,点A,B,C,D在同一条直线上,点E,F分别在直线AD的两侧,且AE=DF,∠A=∠D,AB=DC. 如图,在等边三角形ABC中,AD是高,点G为AD的中点,过G作EF∥AC交AB于点F,交CD于点E,下列说法正确的有①③④(将你认为正确选项的序号都填上).
如图,在等边三角形ABC中,AD是高,点G为AD的中点,过G作EF∥AC交AB于点F,交CD于点E,下列说法正确的有①③④(将你认为正确选项的序号都填上).