��Ŀ����
11����ͼ����ƽ��ֱ������ϵ�У�����������y=kx��ͼ���뷴��������y=$\frac{m}{x}$��ͼ���㣨2��2������1���ֱ��������������ı���ʽ��
��2����ֱ��OA����ƽ��3����λ���Ⱥ���y�ύ��B���뷴��������ͼ���ڵ�һ�����ڵĽ���ΪC������AB��AC�����C�����꼰��ABC�������
��3������������ͼ�����Ƿ���ڵ�D��ʹDC��BC�������ڣ��������D�����ꣻ�������ڣ���˵�����ɣ�
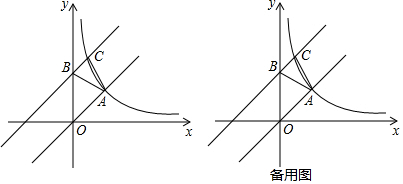
���� ��1������A��2��2�����������������м������k��ֵ���ٽ�A��2��2�����뷴���������м������m��ֵ��
��2���������֪��B������Ϊ��0��3��������ֱ��BC�Ľ���ʽΪy=x+3������ֱ��BC�Ľ���ʽ�뷴���������Ľ���ʽ�������C�����꣬����OC������OA��BC�����ԡ�ABC��������ڡ�BOC�������
��3����D��m��$\frac{4}{m}$��������DC��BC������kDC•kBC=-1���Ӷ��г��������m��ֵ��
��� �⣺��1����A��2��2������y=kx��
��2k=2��
��k=1��
�������������Ľ���ʽΪ��y=x
��A��2��2������y=$\frac{m}{x}$��
��m=2��2=4��
�෴���������Ľ���ʽΪ��y=$\frac{4}{x}$��
��2����ֱ��BC��ֱ��OA����ƽ��3����λ���ã�
��B��0��3��
��ֱ��BC�Ľ���ʽΪ��y=x+3��
����$\left\{\begin{array}{l}{y=x+3}\\{y=\frac{4}{x}}\end{array}\right.$
��ã�$\left\{\begin{array}{l}{x=1}\\{y=4}\end{array}\right.$��$\left\{\begin{array}{l}{x=-4}\\{y=-1}\end{array}\right.$��
�ߵ�C�ڵ�һ���ޣ�
���C��������1��4��
��OA��BC��
��S��ABC=S��BOC=$\frac{1}{2}$��3��4=6��
��3����D��m��$\frac{4}{m}$��
��DC��BC��
��kDC•kBC=-1��
��kDC=$\frac{\frac{4}{m}-4}{m-1}$=$\frac{-4}{m}$��
��$\frac{-4}{m}$��1=-1��
��m=4��
��D��4��1��
���� ���⿼�鷴����������һ�κ������ۺ����⣬����Ĺؼ��Ǹ��ݴ���ϵ���������ͼ��Ľ���ʽ���������ڻ��е����ͣ�

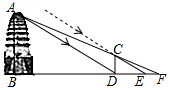 ��ͼ��λ������ʡ�����м������ڵ�С���������й����ڷ�������ʽש���ĵ�����Ʒ������Ϊ˿��֮·��һ����Ҫ��ַ�㣬�����롶�����Ų���¼����С����Сϣ�ȼ�λͬѧ������һЩ�������ߺ���ѧ�ļ���֪ʶ����С�����ĸ߶ȣ����ڹ۲����С�����ײ���ľ��벻�ײ�������˾����о���Ҫ�������β����������������£�������������Ӱ�����в������������£�С����С������Ӱ�Ӷ���D����ֱ��һ��ľ��CD������ô�ʱľ����Ӱ��DE=2.4�ף�Ȼ��Сϣ��BD���ӳ������ҳ�һ��F��ʹ��A��C��F������ͬһֱ���ϣ������DF=2.5�ף���֪ͼ�����е����ͬһƽ���ڣ�ľ����CD=1.72�ף�AB��BF��CD��BF���Ը������ϲ������ݣ���С�����ĸ߶�AB��
��ͼ��λ������ʡ�����м������ڵ�С���������й����ڷ�������ʽש���ĵ�����Ʒ������Ϊ˿��֮·��һ����Ҫ��ַ�㣬�����롶�����Ų���¼����С����Сϣ�ȼ�λͬѧ������һЩ�������ߺ���ѧ�ļ���֪ʶ����С�����ĸ߶ȣ����ڹ۲����С�����ײ���ľ��벻�ײ�������˾����о���Ҫ�������β����������������£�������������Ӱ�����в������������£�С����С������Ӱ�Ӷ���D����ֱ��һ��ľ��CD������ô�ʱľ����Ӱ��DE=2.4�ף�Ȼ��Сϣ��BD���ӳ������ҳ�һ��F��ʹ��A��C��F������ͬһֱ���ϣ������DF=2.5�ף���֪ͼ�����е����ͬһƽ���ڣ�ľ����CD=1.72�ף�AB��BF��CD��BF���Ը������ϲ������ݣ���С�����ĸ߶�AB��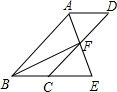 ��ͼ���ı���ABCDΪƽ���ı��Σ���BAD�Ľ�ƽ����AE��CD�ڵ�F����BC���ӳ����ڵ�E������F��AE���е㣬��֤��BF��AF��
��ͼ���ı���ABCDΪƽ���ı��Σ���BAD�Ľ�ƽ����AE��CD�ڵ�F����BC���ӳ����ڵ�E������F��AE���е㣬��֤��BF��AF��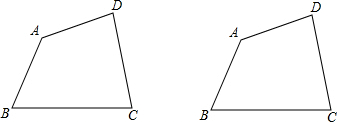
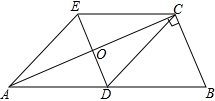 ��ͼ����Rt��ABC�У���BCA=90�㣬CD��AB���ϵ����ߣ��ֱ����C��D��BA��BC��ƽ���ߣ����߽��ڵ�E����DE��AC�ڵ�O������AE��
��ͼ����Rt��ABC�У���BCA=90�㣬CD��AB���ϵ����ߣ��ֱ����C��D��BA��BC��ƽ���ߣ����߽��ڵ�E����DE��AC�ڵ�O������AE��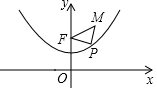 ��֪������y=$\frac{1}{4}$x2+1�����������ʣ���������������һ�㵽����F��0��2���ľ����뵽x��ľ���ʼ����ȣ���ͼ����M������Ϊ��$\sqrt{3}$��3����P��������y=$\frac{1}{4}$x2+1��һ�����㣬���PMF�ܳ�����Сֵ�ǣ�������
��֪������y=$\frac{1}{4}$x2+1�����������ʣ���������������һ�㵽����F��0��2���ľ����뵽x��ľ���ʼ����ȣ���ͼ����M������Ϊ��$\sqrt{3}$��3����P��������y=$\frac{1}{4}$x2+1��һ�����㣬���PMF�ܳ�����Сֵ�ǣ�������