题目内容
1.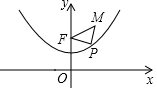 已知抛物线y=$\frac{1}{4}$x2+1具有如下性质:该抛物线上任意一点到定点F(0,2)的距离与到x轴的距离始终相等,如图,点M的坐标为($\sqrt{3}$,3),P是抛物线y=$\frac{1}{4}$x2+1上一个动点,则△PMF周长的最小值是( )
已知抛物线y=$\frac{1}{4}$x2+1具有如下性质:该抛物线上任意一点到定点F(0,2)的距离与到x轴的距离始终相等,如图,点M的坐标为($\sqrt{3}$,3),P是抛物线y=$\frac{1}{4}$x2+1上一个动点,则△PMF周长的最小值是( )| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
分析 过点M作ME⊥x轴于点E,交抛物线y=$\frac{1}{4}$x2+1于点P,由PF=PE结合三角形三边关系,即可得出此时△PMF周长取最小值,再由点F、M的坐标即可得出MF、ME的长度,进而得出△PMF周长的最小值.
解答 解:过点M作ME⊥x轴于点E,交抛物线y=$\frac{1}{4}$x2+1于点P,此时△PMF周长最小值,
∵F(0,2)、M($\sqrt{3}$,3),
∴ME=3,FM=$\sqrt{(\sqrt{3}-0)^{2}+(3-2)^{2}}$=2,
∴△PMF周长的最小值=ME+FM=3+2=5.
故选C.
点评 本题考查了二次函数的性质以及三角形三边关系,根据三角形的三边关系确定点P的位置是解题的关键.

练习册系列答案
相关题目
9.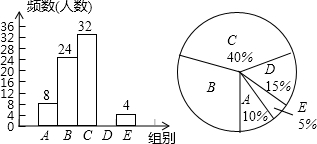 今年4月23日,是第16个世界读书日.某校为了解学生每周课余自主阅读的时间,在本校随机抽取若干名学生进行问卷调查,现将调查结果绘制成如图不完整的统计图表,请根据图表中的信息解答下列问题
今年4月23日,是第16个世界读书日.某校为了解学生每周课余自主阅读的时间,在本校随机抽取若干名学生进行问卷调查,现将调查结果绘制成如图不完整的统计图表,请根据图表中的信息解答下列问题
(1)表中的n=12,中位数落在C组,扇形统计图中B组对应的圆心角为108°;
(2)请补全频数分布直方图;
(3)该校准备召开利用课余时间进行自主阅读的交流会,计划在E组学生中随机选出两人进行经验介绍,已知E组的四名学生中,七、八年级各有1人,九年级有2人,请用画树状图法或列表法求抽取的两名学生都来自九年级的概率.
 今年4月23日,是第16个世界读书日.某校为了解学生每周课余自主阅读的时间,在本校随机抽取若干名学生进行问卷调查,现将调查结果绘制成如图不完整的统计图表,请根据图表中的信息解答下列问题
今年4月23日,是第16个世界读书日.某校为了解学生每周课余自主阅读的时间,在本校随机抽取若干名学生进行问卷调查,现将调查结果绘制成如图不完整的统计图表,请根据图表中的信息解答下列问题| 组别 | 学习时间x(h) | 频数(人数) |
| A | 0<x≤1 | 8 |
| B | 1<x≤2 | 24 |
| C | 2<x≤3 | 32 |
| D | 3<x≤4 | n |
| E | 4小时以上 | 4 |
(2)请补全频数分布直方图;
(3)该校准备召开利用课余时间进行自主阅读的交流会,计划在E组学生中随机选出两人进行经验介绍,已知E组的四名学生中,七、八年级各有1人,九年级有2人,请用画树状图法或列表法求抽取的两名学生都来自九年级的概率.
16.下列命题中,真命题是( )
| A. | 矩形的对角线相互垂直 | |
| B. | 顺次连结对角线相等的四边形各边中点所得到的四边形是矩形 | |
| C. | 等边三角形既是轴对称图形又是中心对称图形 | |
| D. | 对角线互相垂直平分的四边形是菱形 |
13. 如图,平行四边形ABCD内接于⊙O,则∠ADC=( )
如图,平行四边形ABCD内接于⊙O,则∠ADC=( )
 如图,平行四边形ABCD内接于⊙O,则∠ADC=( )
如图,平行四边形ABCD内接于⊙O,则∠ADC=( )| A. | 45° | B. | 50° | C. | 60° | D. | 75° |
10.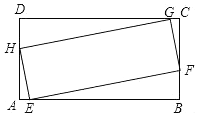 如图,四边形EFGH与四边形ABCD均为矩形,点E,F,G,H分别在边AB,BC,CD,DA上,且EF=3HE,AB=2BC,则tan∠AHE=( )
如图,四边形EFGH与四边形ABCD均为矩形,点E,F,G,H分别在边AB,BC,CD,DA上,且EF=3HE,AB=2BC,则tan∠AHE=( )
 如图,四边形EFGH与四边形ABCD均为矩形,点E,F,G,H分别在边AB,BC,CD,DA上,且EF=3HE,AB=2BC,则tan∠AHE=( )
如图,四边形EFGH与四边形ABCD均为矩形,点E,F,G,H分别在边AB,BC,CD,DA上,且EF=3HE,AB=2BC,则tan∠AHE=( )| A. | $\frac{1}{5}$ | B. | $\frac{1}{6}$ | C. | $\frac{2}{7}$ | D. | $\frac{3}{10}$ |
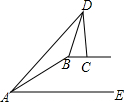 如图,在坡顶B处的同一水平面上有一座纪念碑CD垂直于水平面,小明在斜坡底A处测得该纪念碑顶部D的仰角为45°,然后他沿着坡比i=5:12的斜坡AB攀行了39米到达坡顶,在坡顶B处又测得该纪念碑顶部的仰角为68°.求坡顶B到地面AE的距离和纪念碑CD的高度.(结果精确到1米,参考数据:sin68°=0.9,cos68°=0.4,tan68°=2.5)
如图,在坡顶B处的同一水平面上有一座纪念碑CD垂直于水平面,小明在斜坡底A处测得该纪念碑顶部D的仰角为45°,然后他沿着坡比i=5:12的斜坡AB攀行了39米到达坡顶,在坡顶B处又测得该纪念碑顶部的仰角为68°.求坡顶B到地面AE的距离和纪念碑CD的高度.(结果精确到1米,参考数据:sin68°=0.9,cos68°=0.4,tan68°=2.5) 正方形A1B1C1O,A2B2C2C1,A3B3C3C2…按如图所示放置,点A1、A2、A3…在直线y=x+1上,点C1、C2、C3…在x轴上,则An的坐标是(2n-1-1,2n-1),.
正方形A1B1C1O,A2B2C2C1,A3B3C3C2…按如图所示放置,点A1、A2、A3…在直线y=x+1上,点C1、C2、C3…在x轴上,则An的坐标是(2n-1-1,2n-1),.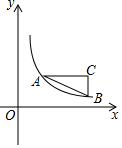 如图,Rt△ABC的两个锐角顶点A,B在函数y=$\frac{k}{x}$(x>0)的图象上,AC∥x轴,AC=2,若点A的坐标为(2,2),则点B的坐标为(4,1).
如图,Rt△ABC的两个锐角顶点A,B在函数y=$\frac{k}{x}$(x>0)的图象上,AC∥x轴,AC=2,若点A的坐标为(2,2),则点B的坐标为(4,1).