题目内容
1.计算:(1)2$\sqrt{12}$×$\frac{\sqrt{3}}{4}$÷5$\sqrt{2}$
(2)($\sqrt{3}$-1)2-(3+$\sqrt{5}$)(3-$\sqrt{5}$).
分析 (1)首先计算开方,然后计算乘法和除法,求出算式的值是多少即可.
(2)首先计算乘方和乘法,然后从左向右依次计算,求出算式的值是多少即可.
解答 解:(1)2$\sqrt{12}$×$\frac{\sqrt{3}}{4}$÷5$\sqrt{2}$
=4$\sqrt{3}$×$\frac{\sqrt{3}}{4}$÷5$\sqrt{2}$
=3÷5$\sqrt{2}$
=$\frac{3\sqrt{2}}{10}$
(2)($\sqrt{3}$-1)2-(3+$\sqrt{5}$)(3-$\sqrt{5}$)
=4-2$\sqrt{3}$-(9-5)
=4-2$\sqrt{3}$-4
=-2$\sqrt{3}$
点评 此题主要考查了二次根式的混合运算,要熟练掌握,解答此题的关键是要明确:①与有理数的混合运算一致,运算顺序先乘方再乘除,最后加减,有括号的先算括号里面的.②在运算中每个根式可以看做是一个“单项式”,多个不同类的二次根式的和可以看作“多项式”.

练习册系列答案
相关题目
20.计算(-a3)2的结果是( )
| A. | a6 | B. | -a6 | C. | -a5 | D. | a5 |
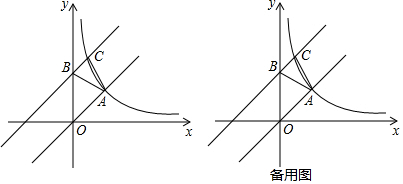
13. 将Rt△AOB 如图放置在直角坐标系中,并绕O点顺时针旋转90°至△COD的位置,已知A(-2,0),∠ABO=30°.则△AOB旋转过程中所扫过的图形的面积为( )
将Rt△AOB 如图放置在直角坐标系中,并绕O点顺时针旋转90°至△COD的位置,已知A(-2,0),∠ABO=30°.则△AOB旋转过程中所扫过的图形的面积为( )
 将Rt△AOB 如图放置在直角坐标系中,并绕O点顺时针旋转90°至△COD的位置,已知A(-2,0),∠ABO=30°.则△AOB旋转过程中所扫过的图形的面积为( )
将Rt△AOB 如图放置在直角坐标系中,并绕O点顺时针旋转90°至△COD的位置,已知A(-2,0),∠ABO=30°.则△AOB旋转过程中所扫过的图形的面积为( )| A. | $\frac{11π}{3}+2\sqrt{3}$ | B. | $3π+2\sqrt{3}$ | C. | $3π+\sqrt{3}$ | D. | $\frac{11π}{3}+\sqrt{3}$ |
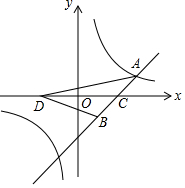 如图,一次函数y=ax-2(a≠0)的图象与反比例函数$y=\frac{k}{x}$(k≠0)的图象交于点A(m,1),且与x轴交于点C.点B(1,-1)在直线AC上.
如图,一次函数y=ax-2(a≠0)的图象与反比例函数$y=\frac{k}{x}$(k≠0)的图象交于点A(m,1),且与x轴交于点C.点B(1,-1)在直线AC上.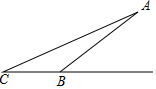 为了游客的安全,某景点将原坡角为30°的斜坡AB改为坡度为1:3的斜坡AC,已知AB=100米,BC在同一水平线上,求改造后斜坡的坡脚向前移动距离BC的长.
为了游客的安全,某景点将原坡角为30°的斜坡AB改为坡度为1:3的斜坡AC,已知AB=100米,BC在同一水平线上,求改造后斜坡的坡脚向前移动距离BC的长.