题目内容
3．已知：四边形ABCD如图所示．（1）填空∠A+∠B+∠C+∠D=360°
（2）请用两种方法证明你的结论．
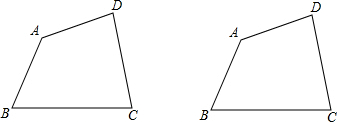
分析 （1）利用四边形的内角和为360°直接回答即可；
（2）转化为三角形的内角和定理求解即可．
解答 解：（1）∠A+∠B+∠C+∠D=360°，
故答案为：360°．
（2）方法一：
连接AC，
把四边形分成两个三角形，
一个三角形内角和为180°，所以两个三角形的内角和为360°，
四边形的内角和是360．
方法二：
∵三角形内角和为180°，
∴4个三角形的内角和为4×180°=720°，
∴四边形内角和为：720°-∠1-∠2-∠3-∠4=720°-360°=360°．
点评 本题考查了多边形的内角和外角，三角形的内角和外角的知识，解题的关键是能够将多边形转化为三角形来求解，难度不大．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
13．
将Rt△AOB 如图放置在直角坐标系中，并绕O点顺时针旋转90°至△COD的位置，已知A（-2，0），∠ABO=30°．则△AOB旋转过程中所扫过的图形的面积为（ ）
将Rt△AOB 如图放置在直角坐标系中，并绕O点顺时针旋转90°至△COD的位置，已知A（-2，0），∠ABO=30°．则△AOB旋转过程中所扫过的图形的面积为（ ）| A． | $\frac{11π}{3}+2\sqrt{3}$ | B． | $3π+2\sqrt{3}$ | C． | $3π+\sqrt{3}$ | D． | $\frac{11π}{3}+\sqrt{3}$ |
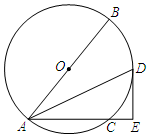如图，⊙O的直径AB=10，弦AC=6，∠BAC的平分线交⊙O于点D，过点D作⊙O的切线交AC的延长线于点E．求DE的长．
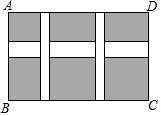如图，某小区规划在一个长40米，宽36米的矩形场地ABCD上修建横、纵道路宽为3：2的三条道路，使其中两条与AB平行，另一条与AD平行，其余部分种草，若使每一块草坪的面积都为198平方米，求道路的宽度．
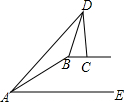如图，在坡顶B处的同一水平面上有一座纪念碑CD垂直于水平面，小明在斜坡底A处测得该纪念碑顶部D的仰角为45°，然后他沿着坡比i=5：12的斜坡AB攀行了39米到达坡顶，在坡顶B处又测得该纪念碑顶部的仰角为68°．求坡顶B到地面AE的距离和纪念碑CD的高度．（结果精确到1米，参考数据：sin68°=0.9，cos68°=0.4，tan68°=2.5）
13．
如图，平行四边形ABCD内接于⊙O，则∠ADC=（ ）
如图，平行四边形ABCD内接于⊙O，则∠ADC=（ ）| A． | 45° | B． | 50° | C． | 60° | D． | 75° |