题目内容
20.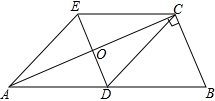 如图,在Rt△ABC中,∠BCA=90°,CD是AB边上的中线,分别过点C,D作BA和BC的平行线,两线交于点E,且DE交AC于点O,连接AE.
如图,在Rt△ABC中,∠BCA=90°,CD是AB边上的中线,分别过点C,D作BA和BC的平行线,两线交于点E,且DE交AC于点O,连接AE.求证:四边形ADCE是菱形.
分析 欲证明四边形ADCE是菱形,需先证明四边形ADCE为平行四边形,然后再证明其对角线相互垂直即可.
解答 证明:∵DE∥BC,EC∥AB,
∴四边形DBCE是平行四边形.
∴EC∥DB,且EC=DB.
在Rt△ABC中,CD为AB边上的中线,
∴AD=DB=CD.
∴EC=AD.
∴四边形ADCE是平行四边形.
∴ED∥BC.
∴∠AOD=∠ACB.
∵∠ACB=90°,
∴∠AOD=∠ACB=90°.
∴平行四边形ADCE是菱形.
点评 本题考查了菱形的判断以及直角三角形斜边上中线的性质,熟记菱形的各种判断方法是解题的关键.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
5.已知下列命题:
①各边相等的多边形是正多边形;
②相等的圆心角所对的弧相等;
③若a2=b2,则a=b;
④若直线y=kx+b经过第一、二、四象限,则k<0,b>0.
其中原命题与逆命题都是真命题的个数是( )
①各边相等的多边形是正多边形;
②相等的圆心角所对的弧相等;
③若a2=b2,则a=b;
④若直线y=kx+b经过第一、二、四象限,则k<0,b>0.
其中原命题与逆命题都是真命题的个数是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
9.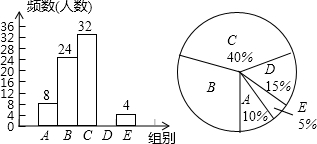 今年4月23日,是第16个世界读书日.某校为了解学生每周课余自主阅读的时间,在本校随机抽取若干名学生进行问卷调查,现将调查结果绘制成如图不完整的统计图表,请根据图表中的信息解答下列问题
今年4月23日,是第16个世界读书日.某校为了解学生每周课余自主阅读的时间,在本校随机抽取若干名学生进行问卷调查,现将调查结果绘制成如图不完整的统计图表,请根据图表中的信息解答下列问题
(1)表中的n=12,中位数落在C组,扇形统计图中B组对应的圆心角为108°;
(2)请补全频数分布直方图;
(3)该校准备召开利用课余时间进行自主阅读的交流会,计划在E组学生中随机选出两人进行经验介绍,已知E组的四名学生中,七、八年级各有1人,九年级有2人,请用画树状图法或列表法求抽取的两名学生都来自九年级的概率.
 今年4月23日,是第16个世界读书日.某校为了解学生每周课余自主阅读的时间,在本校随机抽取若干名学生进行问卷调查,现将调查结果绘制成如图不完整的统计图表,请根据图表中的信息解答下列问题
今年4月23日,是第16个世界读书日.某校为了解学生每周课余自主阅读的时间,在本校随机抽取若干名学生进行问卷调查,现将调查结果绘制成如图不完整的统计图表,请根据图表中的信息解答下列问题| 组别 | 学习时间x(h) | 频数(人数) |
| A | 0<x≤1 | 8 |
| B | 1<x≤2 | 24 |
| C | 2<x≤3 | 32 |
| D | 3<x≤4 | n |
| E | 4小时以上 | 4 |
(2)请补全频数分布直方图;
(3)该校准备召开利用课余时间进行自主阅读的交流会,计划在E组学生中随机选出两人进行经验介绍,已知E组的四名学生中,七、八年级各有1人,九年级有2人,请用画树状图法或列表法求抽取的两名学生都来自九年级的概率.
10.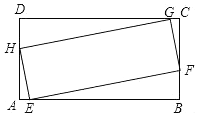 如图,四边形EFGH与四边形ABCD均为矩形,点E,F,G,H分别在边AB,BC,CD,DA上,且EF=3HE,AB=2BC,则tan∠AHE=( )
如图,四边形EFGH与四边形ABCD均为矩形,点E,F,G,H分别在边AB,BC,CD,DA上,且EF=3HE,AB=2BC,则tan∠AHE=( )
 如图,四边形EFGH与四边形ABCD均为矩形,点E,F,G,H分别在边AB,BC,CD,DA上,且EF=3HE,AB=2BC,则tan∠AHE=( )
如图,四边形EFGH与四边形ABCD均为矩形,点E,F,G,H分别在边AB,BC,CD,DA上,且EF=3HE,AB=2BC,则tan∠AHE=( )| A. | $\frac{1}{5}$ | B. | $\frac{1}{6}$ | C. | $\frac{2}{7}$ | D. | $\frac{3}{10}$ |
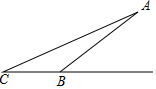 为了游客的安全,某景点将原坡角为30°的斜坡AB改为坡度为1:3的斜坡AC,已知AB=100米,BC在同一水平线上,求改造后斜坡的坡脚向前移动距离BC的长.
为了游客的安全,某景点将原坡角为30°的斜坡AB改为坡度为1:3的斜坡AC,已知AB=100米,BC在同一水平线上,求改造后斜坡的坡脚向前移动距离BC的长.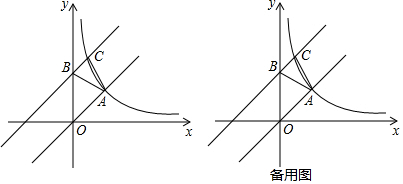
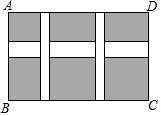 如图,某小区规划在一个长40米,宽36米的矩形场地ABCD上修建横、纵道路宽为3:2的三条道路,使其中两条与AB平行,另一条与AD平行,其余部分种草,若使每一块草坪的面积都为198平方米,求道路的宽度.
如图,某小区规划在一个长40米,宽36米的矩形场地ABCD上修建横、纵道路宽为3:2的三条道路,使其中两条与AB平行,另一条与AD平行,其余部分种草,若使每一块草坪的面积都为198平方米,求道路的宽度.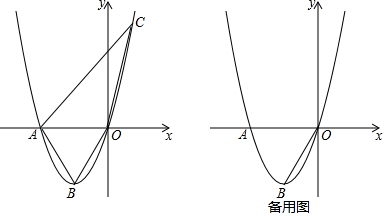
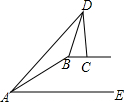 如图,在坡顶B处的同一水平面上有一座纪念碑CD垂直于水平面,小明在斜坡底A处测得该纪念碑顶部D的仰角为45°,然后他沿着坡比i=5:12的斜坡AB攀行了39米到达坡顶,在坡顶B处又测得该纪念碑顶部的仰角为68°.求坡顶B到地面AE的距离和纪念碑CD的高度.(结果精确到1米,参考数据:sin68°=0.9,cos68°=0.4,tan68°=2.5)
如图,在坡顶B处的同一水平面上有一座纪念碑CD垂直于水平面,小明在斜坡底A处测得该纪念碑顶部D的仰角为45°,然后他沿着坡比i=5:12的斜坡AB攀行了39米到达坡顶,在坡顶B处又测得该纪念碑顶部的仰角为68°.求坡顶B到地面AE的距离和纪念碑CD的高度.(结果精确到1米,参考数据:sin68°=0.9,cos68°=0.4,tan68°=2.5)