题目内容
12.已知⊙O的直径为$4\sqrt{5}$cm,弦AB为8cm,P为弦AB上的一动点,若OP的长度为整数,则满足条件的点P有( )| A. | 2个 | B. | 3个 | C. | 5个 | D. | 7个 |
分析 找到两个极值点,点P与点A或点B重合时OP取得最大,此时OP=5,当OP⊥AB时,OP取得最小,从而求出OP的取值范围.
解答  解:①当点P与点A或点P重合时,OP=r=2cm;
解:①当点P与点A或点P重合时,OP=r=2cm;
②如图所示:
∵OP⊥AB,
∴AP=PB=$\frac{1}{2}$AB=4,
在Rt△OPB中,OP=$\sqrt{O{B}^{2}-B{P}^{2}}$=$\sqrt{(2\sqrt{5})^{2}-{4}^{2}}$=2(cm).
综上可得OP的取值范围为:2cm≤OP≤2$\sqrt{5}$cm.
则OP的整数值是2,3,4.其中长度是2cm的只有当OP⊥AB时一种情况,当OP=3cm、4cm各自有2种情况.则总计有5种.
故选C.
点评 本题考查了垂径定理的知识,平分弦的直径平分这条弦,并且平分弦所对的两条弧,需要同学们熟练掌握.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17. 如图所示,一棵大树高8米,一场大风过后,大树在离地面3米处折断倒下,树的顶端落在地上,则此时树的顶端离树的底部有( )米.
如图所示,一棵大树高8米,一场大风过后,大树在离地面3米处折断倒下,树的顶端落在地上,则此时树的顶端离树的底部有( )米.
 如图所示,一棵大树高8米,一场大风过后,大树在离地面3米处折断倒下,树的顶端落在地上,则此时树的顶端离树的底部有( )米.
如图所示,一棵大树高8米,一场大风过后,大树在离地面3米处折断倒下,树的顶端落在地上,则此时树的顶端离树的底部有( )米.| A. | 4 | B. | 3.5 | C. | 5 | D. | 13.6 |
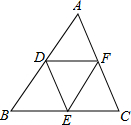 如图,点D,E,F分别是△ABC的AB,BC,CA边的中点.若△DEF的周长为10,则△ABC的周长为20.
如图,点D,E,F分别是△ABC的AB,BC,CA边的中点.若△DEF的周长为10,则△ABC的周长为20. 如图,一根电线杆AB直立于地面,拉线AC=6m,拉线底端C与电线杆底端B的距离为3m,求电线杆AB的高度.
如图,一根电线杆AB直立于地面,拉线AC=6m,拉线底端C与电线杆底端B的距离为3m,求电线杆AB的高度.