题目内容
17．
如图所示，一棵大树高8米，一场大风过后，大树在离地面3米处折断倒下，树的顶端落在地上，则此时树的顶端离树的底部有（ ）米．| A． | 4 | B． | 3.5 | C． | 5 | D． | 13.6 |
分析 根据题意得出AB及AC的长，再由勾股定理即可得出结论．
解答 
解：∵大树高8米，在离地面3米处折断，
∴AB=3米，AC=8-3=5（米），
∴BC=$\sqrt{A{C}^{2}-A{B}^{2}}$=$\sqrt{{5}^{2}-{3}^{2}}$=4（米）．
故选B．
点评 此题是勾股定理的应用，解本题的关键是把实际问题转化为数学问题来解决．此题也可以直接用算术的算法求解．
练习册系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
8．
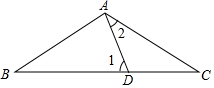已知AB=AC=BD，则∠1与∠2的关系是（ ）
已知AB=AC=BD，则∠1与∠2的关系是（ ）| A． | ∠1=2∠2 | B． | 2∠1+∠2=180° | C． | ∠1+3∠2=180° | D． | 3∠1-∠2=180° |
5．若关于x 的一元二次方程（m-2）2x2+（2m+1）x+1=0有解，那么m的取值范围是（ ）
| A． | m＞$\frac{3}{4}$ | B． | m≥$\frac{3}{4}$ | C． | m＞$\frac{3}{4}$且m≠2 | D． | m≥$\frac{3}{4}$且m≠2 |
2．关于x的方程|x2-2|=m-x有3个互不相同的解，则m的最大值为（ ）
| A． | $\frac{9}{2}$ | B． | $\frac{3}{4}$ | C． | $\frac{9}{4}$ | D． | $\frac{7}{2}$ |
如图，已知抛物线y=-3（x+m）2+k与x轴交于A（1，0），B（3，0）两点，现将抛物线向左平移，记平移后的抛物线顶点为C′，当点C′恰好落在y轴上时，平移后的抛物线解析式为y=-3（x-2）2．