题目内容
3．
如图，一根电线杆AB直立于地面，拉线AC=6m，拉线底端C与电线杆底端B的距离为3m，求电线杆AB的高度．
分析 直接根据勾股定理求解即可．
解答 解：∵AC=6m，BC=3m，AB⊥BC，
∴AB=$\sqrt{A{C}^{2}-B{C}^{2}}$=$\sqrt{{6}^{2}-{3}^{2}}$=3$\sqrt{3}$（m）．
答：电线杆AB的高度为3$\sqrt{3}$m．
点评 本题考查的是勾股定理的应用，解题的关键是利用题目信息构造直角三角形，从而运用勾股定理解题．
练习册系列答案
相关题目
13．⊙O的弦AB的长为8cm，弦AB的弦心距为3cm，则⊙O的半径为（ ）
| A． | 4cm | B． | 5cm | C． | 8cm | D． | 10cm |
14．下列说法中，正确的个数是（ ）
①实数包括有理数、无理数和零；
②一个锐角加上一个钝角等于一平角是真命题；
③幂的乘方，底数不变，指数相加；
④平方根与立方根都等于它本身的数为1和0．
①实数包括有理数、无理数和零；
②一个锐角加上一个钝角等于一平角是真命题；
③幂的乘方，底数不变，指数相加；
④平方根与立方根都等于它本身的数为1和0．
| A． | 3个 | B． | 2个 | C． | 1个 | D． | 0个 |
8．
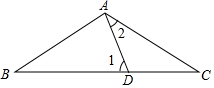已知AB=AC=BD，则∠1与∠2的关系是（ ）
已知AB=AC=BD，则∠1与∠2的关系是（ ）| A． | ∠1=2∠2 | B． | 2∠1+∠2=180° | C． | ∠1+3∠2=180° | D． | 3∠1-∠2=180° |
如图，在△ABE中，点C、D在BE上，BC=AC=CD=AD=DE，求∠BAE的度数？