题目内容
计算:
(1)
-3
+
(2)|-2
|+2
-
-
(3)(1+
)2
(4)(
-
)(
+
)+2
(5)
(6)
.
(1)
| 32 |
|
| 2 |
(2)|-2
| 3 |
|
| 12 |
| 8 |
(3)(1+
| 3 |
(4)(
| 5 |
| 7 |
| 5 |
| 7 |
(5)
|
(6)
|
考点:二次根式的混合运算,解二元一次方程组
专题:计算题
分析:(1)先把各二次根式化为最简二次根式,然后合并即可;
(2)先把各二次根式化为最简二次根式,然后合并即可;
(3)利用完全平方公式计算;
(4)利用平方差公式计算;
(5)先利用加减消元法求出x,然后利用代入法求出y;
(6)先利用加减消元法求出x,然后利用代入法求出y.
(2)先把各二次根式化为最简二次根式,然后合并即可;
(3)利用完全平方公式计算;
(4)利用平方差公式计算;
(5)先利用加减消元法求出x,然后利用代入法求出y;
(6)先利用加减消元法求出x,然后利用代入法求出y.
解答:解:(1)原式=4
-
+
=
;
(2)原式=2
+
-2
-2
=-
;
(3)原式=1+2
+3=4+2
;
(4)原式=5-7+2=0;
(5)
,
①×3+②得6x+x=15+6,
解得x=3,
把x=3代入①得6+y=5,
解得y=-1,
所以方程组的解为
;
(6)
,
①×3+②得6x+4x=6-1,
解得x=
,
把x=
代入①得1+3y=2,
解得y=
,
所以方程组的解为
.
| 2 |
3
| ||
| 2 |
| 2 |
3
| ||
| 2 |
(2)原式=2
| 3 |
| 2 |
| 3 |
| 2 |
| 2 |
(3)原式=1+2
| 3 |
| 3 |
(4)原式=5-7+2=0;
(5)
|
①×3+②得6x+x=15+6,
解得x=3,
把x=3代入①得6+y=5,
解得y=-1,
所以方程组的解为
|
(6)
|
①×3+②得6x+4x=6-1,
解得x=
| 1 |
| 2 |
把x=
| 1 |
| 2 |
解得y=
| 1 |
| 3 |
所以方程组的解为
|
点评:本题考查了二次根式的混合运算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.也考查了解二元一次方程组.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
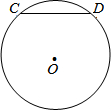 如图,CD是⊙O的弦,且CD=6.根据以上条件你能求出⊙O的半径吗?
如图,CD是⊙O的弦,且CD=6.根据以上条件你能求出⊙O的半径吗?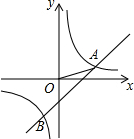 如图,在平面直角坐标系中,O为原点,一次函数y=kx+b与反比例函数
如图,在平面直角坐标系中,O为原点,一次函数y=kx+b与反比例函数
 已知:如图,直线AB与直线CD相交于点O,∠AOD与∠BOC是对顶角.求证:∠AOD=∠BOC.
已知:如图,直线AB与直线CD相交于点O,∠AOD与∠BOC是对顶角.求证:∠AOD=∠BOC. 如图,已知正方形ABCD的边长为2,如果将线段BD绕着点B旋转后,点D落在CB的延长线上的E处,那么AE为
如图,已知正方形ABCD的边长为2,如果将线段BD绕着点B旋转后,点D落在CB的延长线上的E处,那么AE为