题目内容
永州正在创建全国卫生城市,现某校进行大扫除,有大量垃圾需要运送,现租用甲(载重量8吨)、乙(载重量10吨)两种垃圾车共12辆运送,全部车辆运送一次可运送110吨垃圾,
(1)求甲、乙两种垃圾车各有多少辆?
(2)随着大扫除的深入,需要一次运送垃圾165吨以上,为了完成任务,准备新租这两种垃圾车共6辆,共有多少种租用方案,请你一一写出.
(1)求甲、乙两种垃圾车各有多少辆?
(2)随着大扫除的深入,需要一次运送垃圾165吨以上,为了完成任务,准备新租这两种垃圾车共6辆,共有多少种租用方案,请你一一写出.
考点:二元一次方程组的应用,一元一次不等式的应用
专题:
分析:(1)设甲乙两种垃圾车分别有x辆、y辆,根据共有12辆车,全部车辆运送一次可运送110吨垃圾,列方程组求解;
(2)设甲种垃圾车增加了z辆,根据需要一次运送垃圾165吨以上,列不等式求解,然后找出租用方案.
(2)设甲种垃圾车增加了z辆,根据需要一次运送垃圾165吨以上,列不等式求解,然后找出租用方案.
解答:解:(1)设甲乙两种垃圾车分别有x辆、y辆,
根据题意得:
,
解得:
.
答:甲垃圾车有5辆,乙种垃圾车有7辆;
(2)设甲种垃圾车增加了z辆,
依题意得:8(5+z)+10(7+6-z)>165,
解得:z<
,
∵z≥0且为整数,
∴z=0,1,2,
∴6-z=6,5,4,
则共有3种租车方案:①甲种垃圾车不租用,乙种垃圾车租用6辆;
②甲种垃圾车租用1辆,乙种垃圾车租用5辆;
③甲种垃圾车租用2辆,乙种垃圾车租用4辆.
根据题意得:
|
解得:
|
答:甲垃圾车有5辆,乙种垃圾车有7辆;
(2)设甲种垃圾车增加了z辆,
依题意得:8(5+z)+10(7+6-z)>165,
解得:z<
| 5 |
| 2 |
∵z≥0且为整数,
∴z=0,1,2,
∴6-z=6,5,4,
则共有3种租车方案:①甲种垃圾车不租用,乙种垃圾车租用6辆;
②甲种垃圾车租用1辆,乙种垃圾车租用5辆;
③甲种垃圾车租用2辆,乙种垃圾车租用4辆.
点评:本题考查了二元一次方程组的应用和一元一次不等式组的应用,解答本题的关键是读懂题意,设出未知数,找出合适的等量关系和不等关系,列方程求解.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目
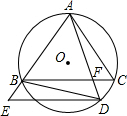 如图,△ABC内接于⊙O,点D在弧BC上,过点D作DE∥BC.交直线AB于点E,连接AD交BC于点F,连接BD,若∠ADB=∠E.
如图,△ABC内接于⊙O,点D在弧BC上,过点D作DE∥BC.交直线AB于点E,连接AD交BC于点F,连接BD,若∠ADB=∠E.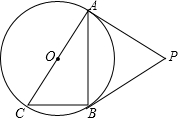 如图,⊙O是Rt△ABC的外接圆,∠ABC=90°,点P是圆外一点,PA切⊙O于点A,且PA=PB.
如图,⊙O是Rt△ABC的外接圆,∠ABC=90°,点P是圆外一点,PA切⊙O于点A,且PA=PB. 如图,AB∥CD,∠1=∠2,∠BEF与∠EFC相等吗?为什么?
如图,AB∥CD,∠1=∠2,∠BEF与∠EFC相等吗?为什么?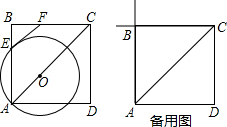 如图,点O在边长为6
如图,点O在边长为6
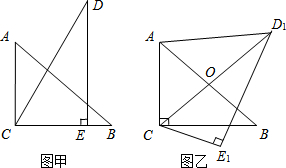 把一副三角板如图甲放置,其中AB=6,DC=7,∠ACB=∠DEC=90°,∠A=45°,∠D=30°,把三角板DCE绕着点C顺时针旋转15°得到△D1CE1(如图乙),此时AB与CD1交于点O,则线段AD1的长度为
把一副三角板如图甲放置,其中AB=6,DC=7,∠ACB=∠DEC=90°,∠A=45°,∠D=30°,把三角板DCE绕着点C顺时针旋转15°得到△D1CE1(如图乙),此时AB与CD1交于点O,则线段AD1的长度为 如图,点D,E都在△ABC的边BC上,∠ABC的平分线垂直于AE,垂足为Q,∠ACB的平分线垂直于AD,垂足为P,连结PQ,若DE=6,则PQ的长为
如图,点D,E都在△ABC的边BC上,∠ABC的平分线垂直于AE,垂足为Q,∠ACB的平分线垂直于AD,垂足为P,连结PQ,若DE=6,则PQ的长为