题目内容
如图,在平面直角坐标系中,四边形OABC是平行四边形,A、B两点的坐标分别是A(3,0),B(0,2).若抛物线y=ax2+bx+c经过点A、B、C,且与x轴的另一个交点为点D.
(1)求抛物线的解析式;
(2)若点P是第二象限内抛物线上一点,直线OP将四边形OBCD的面积分成1:2两部分.求出此时点P的坐标;
(3)设点Q是抛物线对称轴上的一个动点,当点Q的坐标为何值时QD+QC最小?并求出最小值.
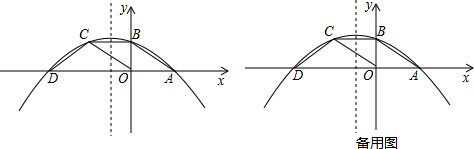
(1)求抛物线的解析式;
(2)若点P是第二象限内抛物线上一点,直线OP将四边形OBCD的面积分成1:2两部分.求出此时点P的坐标;
(3)设点Q是抛物线对称轴上的一个动点,当点Q的坐标为何值时QD+QC最小?并求出最小值.
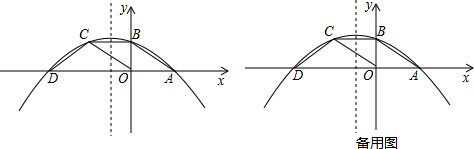
考点:二次函数综合题
专题:
分析:(1)先由平行四边形的性质得出BC=OA=3,BC∥OA,再由B(0,2),得出C(-3,2),然后把A、B、C三点的坐标代入y=ax2+bx+c,运用待定系数法即可求出抛物线的解析式;
(2)先画出图形,计算得出S△OCD=6,S四边形OBCD=9,因此直线OP必经过线段CD.设直线OP与线段CD的交点为E,根据题干可知:△ODE与四边形OBCD的面积比应该是1:2或2:1,即△ODE的面积是四边形OBCD面积的
或
.①当S△ODE=
×9=3时,首先求出直线OE(即直线OP)的解析式,联立抛物线的解析式后即可确定点P的坐标;②当S△ODE=
×9=6时,P与C重合;
(3)连结BD交抛物线的对称轴于点Q,则QD+QC=QD+QB=BD最小,在直角△OBD中运用勾股定理求出BD=2
.运用待定系数法求出直线BD的解析式为y=
x+2,将x=-
代入,求出y的值,即可得到点Q的坐标.
(2)先画出图形,计算得出S△OCD=6,S四边形OBCD=9,因此直线OP必经过线段CD.设直线OP与线段CD的交点为E,根据题干可知:△ODE与四边形OBCD的面积比应该是1:2或2:1,即△ODE的面积是四边形OBCD面积的
| 1 |
| 3 |
| 2 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
(3)连结BD交抛物线的对称轴于点Q,则QD+QC=QD+QB=BD最小,在直角△OBD中运用勾股定理求出BD=2
| 10 |
| 1 |
| 3 |
| 3 |
| 2 |
解答:解:(1)∵四边形OABC是平行四边形,A(3,0),
∴BC=OA=3,BC∥OA.
∵B(0,2),
∴C(-3,2).
把A、B、C三点的坐标代入y=ax2+bx+c,
得
,解得
,
∴抛物线的解析式为y=-
x2-
x+2;
 (2)∵y=-
(2)∵y=-
x2-
x+2,
∴当y=0时,-
x2-
x+2=0,
解得x1=3,x2=-6,
∴D点坐标为(-6,0).
∵S△OCD=
×6×2=6,S四边形OBCD=S△OBC+S△OCD=
×3×2+6=3+6=9,
∴当直线OP将四边形OBCD的面积分成1:2两部分时,设直线OP与直线CD交于点E,则△ODE的面积可以为3或6.
①当S△ODE=
×9=3时,
∵S△ODP=
S△OCD,
∴E为CD的中点,
∵C(-3,2),D(-6,0),
∴E点坐标为(-4.5,1).
设直线OE的解析式为y=kx,则-4.5x=1,
解得k=-
,
∴y=-
x.
设点P的坐标为(x,-
x2-
x+2),
则-
x2-
x+2=-
x,
解得:x1=
,x2=
(舍去),
∴P1(
,
);
②当S△ODE=
×9=6时,P与C重合.
∴P2点坐标为(-3,2).
综上所述,满足条件的点P的坐标为P1(
,
),P2(-3,2);
 (3)如图,连结BD交抛物线的对称轴于点Q,则QD+QC=QD+QB=BD最小,BD=
(3)如图,连结BD交抛物线的对称轴于点Q,则QD+QC=QD+QB=BD最小,BD=
=
=2
.
设直线BD的解析式为y=mx+n,
∵B(0,2),D(-6,0),
∴
,解得
,
∴y=
x+2.
∵抛物线y=-
x2-
x+2的对称轴为x=-
,
∴当x=-
时,y=
×(-
)+2=
,
∴点Q的坐标为(-
,
)时QD+QC最小,此时最小值为2
.
∴BC=OA=3,BC∥OA.
∵B(0,2),
∴C(-3,2).
把A、B、C三点的坐标代入y=ax2+bx+c,
得
|
|
∴抛物线的解析式为y=-
| 1 |
| 9 |
| 1 |
| 3 |
 (2)∵y=-
(2)∵y=-| 1 |
| 9 |
| 1 |
| 3 |
∴当y=0时,-
| 1 |
| 9 |
| 1 |
| 3 |
解得x1=3,x2=-6,
∴D点坐标为(-6,0).
∵S△OCD=
| 1 |
| 2 |
| 1 |
| 2 |
∴当直线OP将四边形OBCD的面积分成1:2两部分时,设直线OP与直线CD交于点E,则△ODE的面积可以为3或6.
①当S△ODE=
| 1 |
| 3 |
∵S△ODP=
| 1 |
| 2 |
∴E为CD的中点,
∵C(-3,2),D(-6,0),
∴E点坐标为(-4.5,1).
设直线OE的解析式为y=kx,则-4.5x=1,
解得k=-
| 2 |
| 9 |
∴y=-
| 2 |
| 9 |
设点P的坐标为(x,-
| 1 |
| 9 |
| 1 |
| 3 |
则-
| 1 |
| 9 |
| 1 |
| 3 |
| 2 |
| 9 |
解得:x1=
-1-
| ||
| 2 |
-1+
| ||
| 2 |
∴P1(
-1-
| ||
| 2 |
1+
| ||
| 9 |
②当S△ODE=
| 2 |
| 3 |
∴P2点坐标为(-3,2).
综上所述,满足条件的点P的坐标为P1(
-1-
| ||
| 2 |
1+
| ||
| 9 |
 (3)如图,连结BD交抛物线的对称轴于点Q,则QD+QC=QD+QB=BD最小,BD=
(3)如图,连结BD交抛物线的对称轴于点Q,则QD+QC=QD+QB=BD最小,BD=| OB2+OD2 |
| 22+62 |
| 10 |
设直线BD的解析式为y=mx+n,
∵B(0,2),D(-6,0),
∴
|
|
∴y=
| 1 |
| 3 |
∵抛物线y=-
| 1 |
| 9 |
| 1 |
| 3 |
| 3 |
| 2 |
∴当x=-
| 3 |
| 2 |
| 1 |
| 3 |
| 3 |
| 2 |
| 3 |
| 2 |
∴点Q的坐标为(-
| 3 |
| 2 |
| 3 |
| 2 |
| 10 |
点评:本题是二次函数的综合题型,其中涉及到的知识点有平行四边形的性质,运用待定系数法求二次函数、一次函数的解析式,二次函数的性质,图形面积的求法,勾股定理,轴对称的性质等知识,综合性较强,难度适中.运用数形结合、分类讨论、方程思想是解题的关键.

练习册系列答案
相关题目
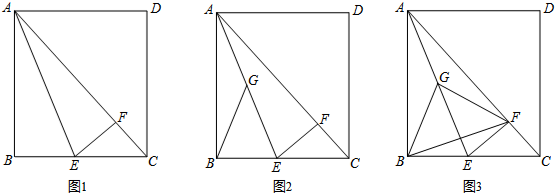
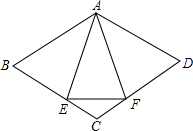 已知:如图,菱形ABCD中,E、F分别是CB、CD上的点,∠BAF=∠DAE.
已知:如图,菱形ABCD中,E、F分别是CB、CD上的点,∠BAF=∠DAE.
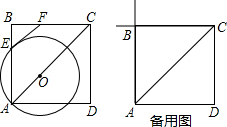 如图,点O在边长为6
如图,点O在边长为6