题目内容
已知二次函数y=a(x-1)2-4的图象经过点(3,0).
(1)求a的值;
(2)若A(m,y1)、B(m+n,y2)(n>0)是该函数图象上的两点,当y1=y2时,求m、n之间的数量关系.
(1)求a的值;
(2)若A(m,y1)、B(m+n,y2)(n>0)是该函数图象上的两点,当y1=y2时,求m、n之间的数量关系.
考点:二次函数图象上点的坐标特征
专题:
分析:(1)把点(3,0)的坐标代入函数解析式计算即可得解;
(2)方法一:根据y1=y2列出关于m、n的方程,然后开方整理即可得解;
方法二:根据二次函数的对称性列出关于m、n的方程,然后整理即可得解.
(2)方法一:根据y1=y2列出关于m、n的方程,然后开方整理即可得解;
方法二:根据二次函数的对称性列出关于m、n的方程,然后整理即可得解.
解答:解:(1)将(3,0)代入y=a(x-1)2-4,得0=4a-4,
解得a=1;
(2)方法一:根据题意,得y1=(m-1)2-4,y2=(m+n-1)2-4,
∵y1=y2,
∴(m-1)2-4=(m+n-1)2-4,
即(m-1)2=(m+n-1)2,
∵n>0,
∴m-1=-(m+n-1),
化简,得2m+n=2;
方法二:∵函数y=(x-1)2-4的图象的对称轴是经过点(1,-4),且平行于y轴的直线,
∴m+n-1=1-m,
化简,得2m+n=2.
解得a=1;
(2)方法一:根据题意,得y1=(m-1)2-4,y2=(m+n-1)2-4,
∵y1=y2,
∴(m-1)2-4=(m+n-1)2-4,
即(m-1)2=(m+n-1)2,
∵n>0,
∴m-1=-(m+n-1),
化简,得2m+n=2;
方法二:∵函数y=(x-1)2-4的图象的对称轴是经过点(1,-4),且平行于y轴的直线,
∴m+n-1=1-m,
化简,得2m+n=2.
点评:本题考查了二次函数图象上点的坐标特征,主要是待定系数法求二次函数解析式的思想的渗透,二次函数的对称性的应用.

练习册系列答案
相关题目
平行四边形的对角线( )
| A、相等 | B、不相等 |
| C、互相平分 | D、互相垂直 |
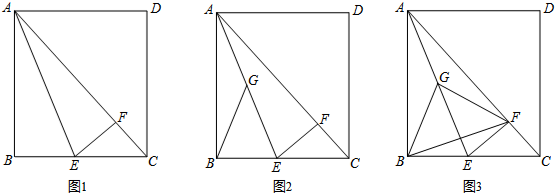
 如图,O是菱形ABCD对角线AC与BD的交点,CD=5cm,OD=3cm;过点C作CE∥DB,过点B作BE∥AC,CE与BE相交于点E.
如图,O是菱形ABCD对角线AC与BD的交点,CD=5cm,OD=3cm;过点C作CE∥DB,过点B作BE∥AC,CE与BE相交于点E.
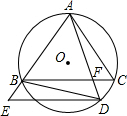 如图,△ABC内接于⊙O,点D在弧BC上,过点D作DE∥BC.交直线AB于点E,连接AD交BC于点F,连接BD,若∠ADB=∠E.
如图,△ABC内接于⊙O,点D在弧BC上,过点D作DE∥BC.交直线AB于点E,连接AD交BC于点F,连接BD,若∠ADB=∠E.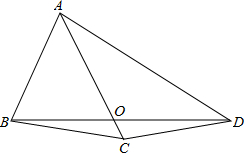 如图,在四边形ABCD中,线段AC、BD相交于O,AB=BC=CD,∠ABC=70°,∠BCD=170°,求∠BAD的度数.
如图,在四边形ABCD中,线段AC、BD相交于O,AB=BC=CD,∠ABC=70°,∠BCD=170°,求∠BAD的度数.