题目内容

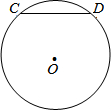如图，CD是⊙O的弦，且CD=6．根据以上条件你能求出⊙O的半径吗？
考点：垂径定理,勾股定理
专题：
分析：作OH⊥CD于H，连结OC，根据垂径定理得CH=
1
2
CD=3，再根据勾股定理得OC=
9+OH2
，由于OH不能确定，所以不能求出OC的长．
解答：解：作OH⊥CD于H，连结OC，如图，
∴CH=DH=
1
2
CD=3，
∴OC=
CH2+OH2
=
9+OH2
，
∵OH不能确定，
∴不能求出OC的长，
∴根据以上条件不能求出⊙O的半径．
点评：本题考查了垂径定理：平分弦的直径平分这条弦，并且平分弦所对的两条弧．也考查了勾股定理．
练习册系列答案
相关题目
平行四边形的对角线（　　）
A、相等B、不相等
C、互相平分D、互相垂直
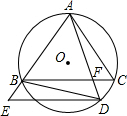如图，△ABC内接于⊙O，点D在弧BC上，过点D作DE∥BC．交直线AB于点E，连接AD交BC于点F，连接BD，若∠ADB=∠E．
（1）求证：AB=AC；
（2）若AD=2
5
，BE=1，求AF的长度．
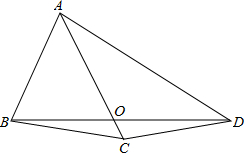如图，在四边形ABCD中，线段AC、BD相交于O，AB=BC=CD，∠ABC=70°，∠BCD=170°，求∠BAD的度数．
如图，过点A（0，3）的直线l1与x轴交于点B，tan∠ABO=
3
4
．过点A的另一直线l2：y=-
3
4t
x+b （t＞0）与x轴交于点Q，点P是射线AB上的一个动点，过P作PH⊥x轴于点H，设PB=5t．
（1）求直线l1的函数解析式；
（2）当点P在线段AB上运动时，设△PHQ的面积为S（S≠0），求S与t之间的函数关系式（要求写出自变量t的取值范围）；
（3）当点P 在射线AB上运动时，是否存在这样的t值，使以P，H，Q为顶点的三角形与△AOQ相似？若存在，直接写出所有满足条件的t值所对应的P点坐标；若不存在，请说明理由．
解方程：
x-3
x-5
+1=
3
5-x
．
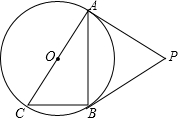如图，⊙O是Rt△ABC的外接圆，∠ABC=90°，点P是圆外一点，PA切⊙O于点A，且PA=PB．
（1）求证：PB是⊙O的切线；
（2）已知PA=
3
，∠ACB=60°，求⊙O的半径．
计算：
（1）
32
-3
1
2
+
2

（2）|-2
3
|+2
1
2
-
12
-
8

（3）（1+
3
）2 
（4）(
5
-
7
)(
5
+
7
)+2               
（5）
2x+y=5
x-3y=6

（6）
2x+3y=2
4x-9y=-1
．
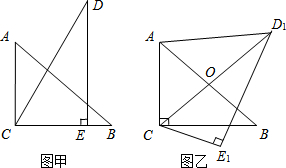把一副三角板如图甲放置，其中AB=6，DC=7，∠ACB=∠DEC=90°，∠A=45°，∠D=30°，把三角板DCE绕着点C顺时针旋转15°得到△D1CE1（如图乙），此时AB与CD1交于点O，则线段AD1的长度为
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网