题目内容
8.关于x的分式方程$\frac{5}{x}=\frac{a}{x-2}$有解,则字母a的取值范围是a≠5,a≠0.分析 先解关于x的分式方程,求得x的值,然后再依据“关于x的分式方程$\frac{5}{x}=\frac{a}{x-2}$有解”,即x≠0且x≠2建立不等式即可求a的取值范围.
解答 解:方程$\frac{5}{x}=\frac{a}{x-2}$
去分母得:5(x-2)=ax,
去括号得:5x-10=ax,
移项,合并同类项得:
(5-a)x=10,
∵关于x的分式方程$\frac{5}{x}=\frac{a}{x-2}$有解,
∴5-a≠0,x≠0且x≠2,
即a≠5,
系数化为1得:x=$\frac{10}{5-a}$,
∴$\frac{10}{5-a}$≠0且$\frac{10}{5-a}$≠2,
即a≠5,a≠0,综上所述:关于x的分式方程$\frac{5}{x}=\frac{a}{x-2}$有解,则字母a的取值范围是a≠5,a≠0,
故答案为:a≠5,a≠0.
点评 此题考查了求分式方程的解,由于我们的目的是求a的取值范围,根据方程的解列出关于a的不等式.另外,解答本题时,容易漏掉5-a≠0,这应引起同学们的足够重视.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
13. 已知如图,△ABC中,AB=AC,AB的垂直平分线交AC于D,△ABC和△DBC的周长分别是60cm和38cm,则△ABC的腰和底边长分别为( )
已知如图,△ABC中,AB=AC,AB的垂直平分线交AC于D,△ABC和△DBC的周长分别是60cm和38cm,则△ABC的腰和底边长分别为( )
 已知如图,△ABC中,AB=AC,AB的垂直平分线交AC于D,△ABC和△DBC的周长分别是60cm和38cm,则△ABC的腰和底边长分别为( )
已知如图,△ABC中,AB=AC,AB的垂直平分线交AC于D,△ABC和△DBC的周长分别是60cm和38cm,则△ABC的腰和底边长分别为( )| A. | 24cm和12cm | B. | 16cm和22cm | C. | 20cm和16cm | D. | 22cm和16cm |
 已知:如图,正方形ABCD的边长为6,BM,DN分别平分正方形的两个外角,且满足∠MAN=45°,连接MC,NC,MN.
已知:如图,正方形ABCD的边长为6,BM,DN分别平分正方形的两个外角,且满足∠MAN=45°,连接MC,NC,MN. 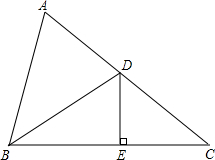 如图:△ABC中,BA=BD,DE垂直平分BC,∠ABD=40°,则∠C=35°.
如图:△ABC中,BA=BD,DE垂直平分BC,∠ABD=40°,则∠C=35°. 如图,在△ABC中,AB的垂直平分线分别交AB,AC于D,E两点,若AC=9cm,BC=5cm,则△BCE的周长为14cm.
如图,在△ABC中,AB的垂直平分线分别交AB,AC于D,E两点,若AC=9cm,BC=5cm,则△BCE的周长为14cm.
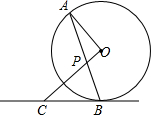 如图,AB是⊙O的弦,OP⊥OA交AB于点P,过点B的⊙O的切线交OP的延长线于点C.
如图,AB是⊙O的弦,OP⊥OA交AB于点P,过点B的⊙O的切线交OP的延长线于点C.