题目内容
19．
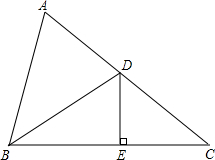如图：△ABC中，BA=BD，DE垂直平分BC，∠ABD=40°，则∠C=35°．
分析 根据三角形内角和定理和等腰三角形性质求出∠BDA，根据线段垂直平分线得出BD=DC，求出∠C=∠CBD，根据三角形外角性质求出∠BDA=2∠C，代入求出即可．
解答 解：∵AB=AD，∠ABD=40°，
∴∠BDA=∠A=$\frac{1}{2}$（180°-∠ABD）=70°，
∵DE垂直平分BC，
∴BD=DC，
∴∠C=∠DBC，
∴∠BDA=∠C+∠CBD=2∠C=70°，
∴∠C=35°
故答案为：35°．
点评 本题考查了三角形内角和定理，等腰三角形性质，线段垂直平分线性质的应用，能求出∠BDA的度数和BD=CD是解此题的关键，注意：线段垂直平分线上的点到线段两个端点的距离相等．
练习册系列答案
相关题目
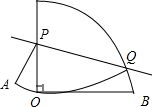如图，是一个圆心角为90°的扇形，AO=2cm，点P在半径AO上运动，点Q在弧AB上运动，沿PQ将它以上的部分向下翻折，使翻折后的弧恰好过点O，则OP的最大距离为$\frac{2\sqrt{3}}{3}$．
如图，若双曲线y=$\frac{k}{x}$与边长为5的等边△AOB的边OA、AB分别相交于C、D两点，且OC=3BD．则实数k的值为$\frac{9\sqrt{3}}{4}$．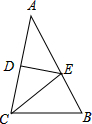
如图，ED为△ABC的AC边的垂直平分线，且AB=5，△BCE的周长为8，则BC的长度为（ ）