题目内容
3.探究问题:(1)方法感悟:
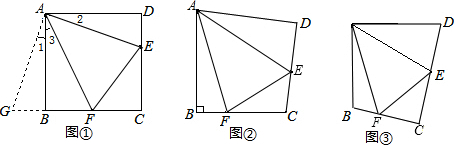
如图①,在正方形ABCD中,点E,F分别为DC,BC边上的点,且满足∠EAF=45°,连接EF,求证DE+BF=EF.
感悟解题方法,并完成下列填空:
将△ADE绕点A顺时针旋转90°得到△ABG,此时AB与AD重合,由旋转可得:AB=AD,BG=DE,∠1=∠2,∠ABG=∠D=90°,∴∠ABG+∠ABF=90°+90°=180°,因此,点G,B,F在同一条直线上.∵∠EAF=45°∴∠2+∠3=∠BAD-∠EAF=90°-45°=45°.∵∠1=∠2,∴∠1+∠3=45°.即∠GAF=∠EAF.又AG=AE,AF=AF∴△GAF≌△EAF.∴GF=EF,故DE+BF=EF.
(2)方法迁移:
如图②,将Rt△ABC沿斜边翻折得到△ADC,点E,F分别为DC,BC边上的点,且∠EAF=$\frac{1}{2}$∠DAB.试猜想DE,BF,EF之间有何数量关系,并证明你的猜想.
(3)问题拓展:
如图③,在四边形ABCD中,AB=AD,E,F分别为DC,BC上的点,满足∠EAF=$\frac{1}{2}$∠DAB,试猜想当∠B与∠D满足什么关系时,可使得DE+BF=EF.请直接写出你的猜想(不必说明理由).
分析 (1)根据旋转变换的性质和全等三角形的判定定理证明△GAF≌△EAF,得到GF=EF,证明结论;
(2)假设∠BAD的度数为m,根据旋转变换的性质证明∠GAF=∠EAF,证明△GAF≌△EAF,得到GF=EF,证明结论;
(3)根据(2)的结论解答即可.
解答 解:(1)AB=AD,BG=DE,∠1=∠2,∠ABG=∠D=90°,
∴∠ABG+∠ABF=90°+90°=180°,
因此,点G,B,F在同一条直线上.
∵∠EAF=45°,
∴∠2+∠3=∠BAD-∠EAF=90°-45°=45°,
∵∠1=∠2,∴∠1+∠3=45°.即∠GAF=∠EAF.
在△GAF和△EAF中,
$\left\{\begin{array}{l}{AG=AE}\\{∠GAF=∠EAF}\\{AF=AF}\end{array}\right.$,
∴△GAF≌△EAF,
∴GF=EF,
故DE+BF=EF;
故答案为:EAF;△EAF;GF;
(2)DE+BF=EF,证明如下:
假设∠BAD的度数为m,将△ADE绕点A顺时针旋转m°得到△ABG,此时AB与AD重合,
由旋转可得:
AB=AD,BG=DE,∠1=∠2,∠ABG=∠D=90°,
∴∠ABG+∠ABF=90°+90°=180°,
∴点G,B,F在同一条直线上,
∵∠EAF=$\frac{1}{2}$m°,
∴∠2+∠3=∠BAD-∠EAF,
即m°-$\frac{1}{2}$m°=$\frac{1}{2}$m°,
∵∠1=∠2,
∴∠1+∠3=$\frac{1}{2}$m°,
即∠GAF=∠EAF,
又∵AG=AE,AF=AF,
∴△GAF≌△EAF(SAS),
∴GF=EF,
又∵GF=BG+BF=DE+BF,
∴DE+BF=EF;
(3)由(2)的结论可知,当∠B与∠D互补时,可使得DE+BF=EF.
点评 本题考查的是正方形的性质、全等三角形的判定和性质、旋转变换的性质,掌握全等三角形的判定定理和性质定理以及旋转变换的性质是解题的关键.

 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案| A. | $\sqrt{5}$ | B. | $\frac{4\sqrt{5}}{5}$ | C. | 2$\sqrt{5}$ | D. | $\frac{2\sqrt{5}}{3}$ |
 如图,若双曲线y=$\frac{k}{x}$与边长为5的等边△AOB的边OA、AB分别相交于C、D两点,且OC=3BD.则实数k的值为$\frac{9\sqrt{3}}{4}$.
如图,若双曲线y=$\frac{k}{x}$与边长为5的等边△AOB的边OA、AB分别相交于C、D两点,且OC=3BD.则实数k的值为$\frac{9\sqrt{3}}{4}$.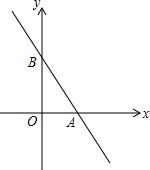 已知一次函数y=kx+b图象与x轴、y轴的交点为A、B两点,且当x=1,y=2;当x=-1,y=6.
已知一次函数y=kx+b图象与x轴、y轴的交点为A、B两点,且当x=1,y=2;当x=-1,y=6. 如图,在△ABC中,BA=BC=20cm,AC=30cm,点P从A出发,沿AB以4cm/s的速度向点B运动;同时点Q从C点出发,沿CA以3cm/s的速度向A点运动.设运动时间为x(s).
如图,在△ABC中,BA=BC=20cm,AC=30cm,点P从A出发,沿AB以4cm/s的速度向点B运动;同时点Q从C点出发,沿CA以3cm/s的速度向A点运动.设运动时间为x(s).