题目内容
17.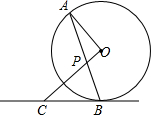 如图,AB是⊙O的弦,OP⊥OA交AB于点P,过点B的⊙O的切线交OP的延长线于点C.
如图,AB是⊙O的弦,OP⊥OA交AB于点P,过点B的⊙O的切线交OP的延长线于点C.(1)求证:CP=CB;
(2)若⊙O的半径为3,OC=5,求点O到AB的距离.
分析 (1)要证明RP=RQ,需要证明∠PQR=∠RPQ,连接OQ,则∠OQR=90°;根据OB=OQ,得∠B=∠OQB,再根据等角的余角相等即可证明;
(2)过O作OD⊥AB于D,根据BC是⊙O的切线,得到∠OBC=90°,由勾股定理得到BC=$\sqrt{O{C}^{2}-O{B}^{2}}$=$\sqrt{{5}^{2}-{3}^{2}}$=4,求得PC=BC=4,OP=1,由勾股定理得到AP=$\sqrt{A{O}^{2}+O{P}^{2}}$=$\sqrt{26}$,求出AD=$\frac{25}{\sqrt{26}}$=$\frac{25\sqrt{26}}{26}$,然后由勾股定理即可得到结论.
解答 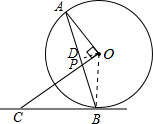 (1)证明:连接OB,
(1)证明:连接OB,
∵BC是⊙O的切线,
∴∠OBA+∠ABC=90°,
∵OP⊥OA,
∴∠OPA+∠A=90°,
又∵OB=OA,
∴∠A=∠OBA,
∴∠ABC=∠OPA=∠CPB,
∴CP=CB;
(2)解:过O作OD⊥AB于D,
∵BC是⊙O的切线,
∴∠OBC=90°,
∴BC=$\sqrt{O{C}^{2}-O{B}^{2}}$=$\sqrt{{5}^{2}-{3}^{2}}$=4,
∴PC=BC=4,
∴OP=1,
∵∠AOP=90°,
∴AP=$\sqrt{A{O}^{2}+O{P}^{2}}$=$\sqrt{26}$,
∴AO2=AP•AD,
∴AD=$\frac{25}{\sqrt{26}}$=$\frac{25\sqrt{26}}{26}$,
∴OD=$\sqrt{A{O}^{2}-A{D}^{2}}$=$\frac{5\sqrt{26}}{26}$.
点评 本题考查了切线的性质,勾股定理,等腰三角形的判定和性质,正确的作出辅助线是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目
6.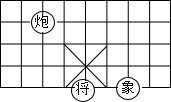 如图所示,若在某棋盘上建立直角坐标系,使“将”位于点(2,-2),“象”位于点(4,-2),则“炮”位于点( )
如图所示,若在某棋盘上建立直角坐标系,使“将”位于点(2,-2),“象”位于点(4,-2),则“炮”位于点( )
 如图所示,若在某棋盘上建立直角坐标系,使“将”位于点(2,-2),“象”位于点(4,-2),则“炮”位于点( )
如图所示,若在某棋盘上建立直角坐标系,使“将”位于点(2,-2),“象”位于点(4,-2),则“炮”位于点( )| A. | (1,3) | B. | (0,1) | C. | (-1,2) | D. | (-2,2) |
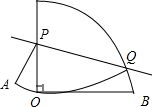 如图,是一个圆心角为90°的扇形,AO=2cm,点P在半径AO上运动,点Q在弧AB上运动,沿PQ将它以上的部分向下翻折,使翻折后的弧恰好过点O,则OP的最大距离为$\frac{2\sqrt{3}}{3}$.
如图,是一个圆心角为90°的扇形,AO=2cm,点P在半径AO上运动,点Q在弧AB上运动,沿PQ将它以上的部分向下翻折,使翻折后的弧恰好过点O,则OP的最大距离为$\frac{2\sqrt{3}}{3}$. 如图,在△ABC中,BA=BC=20cm,AC=30cm,点P从A出发,沿AB以4cm/s的速度向点B运动;同时点Q从C点出发,沿CA以3cm/s的速度向A点运动.设运动时间为x(s).
如图,在△ABC中,BA=BC=20cm,AC=30cm,点P从A出发,沿AB以4cm/s的速度向点B运动;同时点Q从C点出发,沿CA以3cm/s的速度向A点运动.设运动时间为x(s).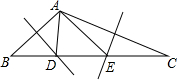 如图,在△ABC中,边AB、AC的垂直平分线分别交BC于D、E.
如图,在△ABC中,边AB、AC的垂直平分线分别交BC于D、E.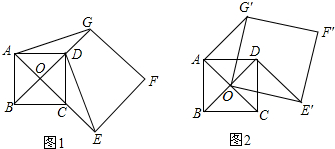
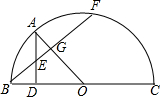 如图所示,BC是半圆O的直径,AD⊥BC,垂足为D,AB弧长等于AF弧长,BF与AD、AO分别交于点E、G.
如图所示,BC是半圆O的直径,AD⊥BC,垂足为D,AB弧长等于AF弧长,BF与AD、AO分别交于点E、G.