题目内容
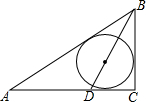 如图所示的△ABC是从工厂中大量存放的铁板余料,小明测得∠C=90°,∠A的平分线分对边BC所得的两条线段分别为BD=5,DC=3,现要最大限度地利用这块余料截出一个圆形铁板.
如图所示的△ABC是从工厂中大量存放的铁板余料,小明测得∠C=90°,∠A的平分线分对边BC所得的两条线段分别为BD=5,DC=3,现要最大限度地利用这块余料截出一个圆形铁板.(1)使用直尺和圆规确定圆形铁板的圆心O;
(2)求圆O的最大半径.
考点:三角形的内切圆与内心
专题:应用题
分析:(1)根据内心的定义作∠ACB的角平分线,两角平分线的交点即为圆形铁板的圆心O;
(2)先根据角平分线定理得
=
=
,设AB=5a,则AC=3a,根据勾股定理得BC=4a,则4a=8,解得a=2,所以AB=10,AC=6,然后利用直角边为a、b,斜边为c的三角形的内切圆半径为
求△ABC的内切圆的半径.
(2)先根据角平分线定理得
| AB |
| AC |
| BD |
| CD |
| 5 |
| 3 |
| a+b-c |
| 2 |
解答:解:(1)作∠ACB的角平分线交BD于点O,则点O为铁板的内切圆的圆心,如图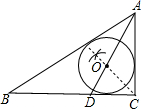 ;
;
(2)∵AD平分∠BAC,
∴
=
=
,
设AB=5a,则AC=3a,
在Rt△ABC中,BC=
=4a,
而BC=BD+CD=8,
∴4a=8,解得a=2,
∴AB=10,AC=6,
∴△ABC的内切圆的半径=
=2,
即圆O的最大半径为2.
 ;
;(2)∵AD平分∠BAC,
∴
| AB |
| AC |
| BD |
| CD |
| 5 |
| 3 |
设AB=5a,则AC=3a,
在Rt△ABC中,BC=
| AB2-AC2 |
而BC=BD+CD=8,
∴4a=8,解得a=2,
∴AB=10,AC=6,
∴△ABC的内切圆的半径=
| 6+8-10 |
| 2 |
即圆O的最大半径为2.
点评:本题考查了三角形的内切圆与内心:与三角形各边都相切的圆叫三角形的内切圆,三角形的内切圆的圆心叫做三角形的内心,这个三角形叫做圆的外切三角形.三角形的内心就是三角形三个内角角平分线的交点.也考查了勾股定理的逆定理.记住直角边为a、b,斜边为c的三角形的内切圆半径为
.
| a+b-c |
| 2 |

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
下列四个函数中,y随x的增大而减小的是( )
| A、y=4x |
| B、y=2x-5 |
| C、y=x-7 |
| D、y=-x+2 |
已知(20x-33)(5x-6)-(14x-20)(5x-6)可以因式分解为(ax+b)(6x+c),其中a,b,c均为整数,则a+b-c的值为( )
| A、12 | B、14 |
| C、-12 | D、-14 |
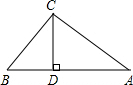 如图,在Rt△ABC中,∠BCA=90°,CD⊥AB,AD=2,CD=2
如图,在Rt△ABC中,∠BCA=90°,CD⊥AB,AD=2,CD=2 如图,在边长相同的小正方形组成的网格中,点A、B、C、D都在这些小正方形的顶点上,AB、CD相交于点P,则cos∠CPB的值是
如图,在边长相同的小正方形组成的网格中,点A、B、C、D都在这些小正方形的顶点上,AB、CD相交于点P,则cos∠CPB的值是