题目内容
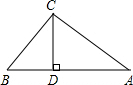 如图,在Rt△ABC中,∠BCA=90°,CD⊥AB,AD=2,CD=2
如图,在Rt△ABC中,∠BCA=90°,CD⊥AB,AD=2,CD=2| 3 |
考点:解直角三角形
专题:计算题
分析:在直角三角形ACD中,由AD与CD的长,利用勾股定理求出AC的长,利用两对角相等的三角形相似得到三角形ACD与三角形ABC相似,由相似得比例求出AB的长,在直角三角形ABC中,利用直角边等于斜边的一半得到∠B的度数,进而求出∠A的度数,即可确定出其他的锐角.
解答:解:在Rt△ACD中,AD=2,CD=2
,
根据勾股定理得:AC=
=4,
∵∠ADC=∠ACB=90°,∠A=∠A,
∴△ACD∽△ABC,
∴
=
,即AC2=AD•AB,
∴16=2AB,即AB=8,
在Rt△ABC中,AC=
AB,
∴∠B=∠ACD=30°,∠A=∠BCD=60°,
| 3 |
根据勾股定理得:AC=
| AD2+CD2 |
∵∠ADC=∠ACB=90°,∠A=∠A,
∴△ACD∽△ABC,
∴
| AC |
| AB |
| AD |
| AC |
∴16=2AB,即AB=8,
在Rt△ABC中,AC=
| 1 |
| 2 |
∴∠B=∠ACD=30°,∠A=∠BCD=60°,
点评:此题考查了解直角三角形,涉及的知识有:勾股定理,相似三角形的判定与性质,含30度直角三角形的性质,熟练掌握相似三角形的判定与性质是解本题的关键.

练习册系列答案
 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
某市2013年生产总值(GDP)比2012年增长了12%,由于受到国际金融危机的影响,预计今年比2013年增长7%.若这两年GDP年平均增长率为x%,则x%满足的关系是( )
| A、12%+7%=x% |
| B、(1+12%)(1+7%)=2(1+x%) |
| C、12%+7%=2•x% |
| D、(1+12%)(1+7%)=(1+x%)2 |
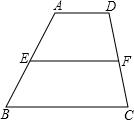 如图,四边形ABCD中,AD∥BC,E是AB上一点,EF∥BC交CD于F.若AD=2,BC=4.5,当AE:EB等于多少时,EF分四边形ABCD所成的两个小四边形相似?
如图,四边形ABCD中,AD∥BC,E是AB上一点,EF∥BC交CD于F.若AD=2,BC=4.5,当AE:EB等于多少时,EF分四边形ABCD所成的两个小四边形相似?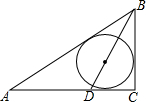 如图所示的△ABC是从工厂中大量存放的铁板余料,小明测得∠C=90°,∠A的平分线分对边BC所得的两条线段分别为BD=5,DC=3,现要最大限度地利用这块余料截出一个圆形铁板.
如图所示的△ABC是从工厂中大量存放的铁板余料,小明测得∠C=90°,∠A的平分线分对边BC所得的两条线段分别为BD=5,DC=3,现要最大限度地利用这块余料截出一个圆形铁板.