题目内容
如图，在边长相同的小正方形组成的网格中，点A、B、C、D都在这些小正方形的顶点上，AB、CD相交于点P，则cos∠CPB的值是考点：相似三角形的判定与性质,勾股定理,锐角三角函数的定义
专题：网格型
分析：如图，连接AE，交CD于点F，可先证得△APC∽△BPD，可得到CP：DP=1：3，且可得CF=DF=AF，可知FP：DF=1：2，在Rt△AFP中可求得cos∠APF，且∠CPB=∠APF，可得出答案．
解答：
解：如图，连接AE，交CD于点F，
∵AC∥BD，且BD=3AC，
∴
=
=
，
又∵四边形ACED为正方形，
∴AE⊥CD，DF=CF，
∴
=
，
∴
=
，
在Rt△APF中，设PF=x，则AF=2x，由勾股定理可求得AP=
x，
∴
=
=
，
∴cos∠APF=
，
又∵∠CPB=∠APF，
∴cos∠CPB=
．
故答案为：
．
解：如图，连接AE，交CD于点F，∵AC∥BD，且BD=3AC，
∴
| CP |
| DP |
| AC |
| BD |
| 1 |
| 3 |
又∵四边形ACED为正方形，
∴AE⊥CD，DF=CF，
∴
| PF |
| DF |
| 1 |
| 2 |
∴
| PF |
| AF |
| 1 |
| 2 |
在Rt△APF中，设PF=x，则AF=2x，由勾股定理可求得AP=
| 5 |
∴
| PF |
| AP |
| x | ||
|
| ||
| 5 |
∴cos∠APF=
| ||
| 5 |
又∵∠CPB=∠APF，
∴cos∠CPB=
| ||
| 5 |
故答案为：
| ||
| 5 |
点评：此题考查了相似三角形的判定与性质与三角函数的定义．此题难度适中，解题的关键是准确作出辅助线，注意转化思想与数形结合思想的应用．
练习册系列答案
学业测评一课一测系列答案
小学课时作业全通练案系列答案
相关题目
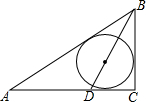如图所示的△ABC是从工厂中大量存放的铁板余料，小明测得∠C=90°，∠A的平分线分对边BC所得的两条线段分别为BD=5，DC=3，现要最大限度地利用这块余料截出一个圆形铁板．