题目内容
已知（20x-33）（5x-6）-（14x-20）（5x-6）可以因式分解为（ax+b）（6x+c），其中a，b，c均为整数，则a+b-c的值为（ ）
| A、12 | B、14 |
| C、-12 | D、-14 |
考点：因式分解-提公因式法
专题：计算题
分析：根据题意列出等式，分解因式后确定出a，b，c的值，即可求出a+b-c的值．
解答：解：（20x-33）（5x-6）-（14x-20）（5x-6）=（5x-6）（20x-33-14x+20）=（5x-6）（6x-13）=（ax+b）（6x+c），
可得a=5，b=-6，c=-13，
则a+b-c=5-6+13=12．
故选A．
可得a=5，b=-6，c=-13，
则a+b-c=5-6+13=12．
故选A．
点评：此题考查了因式分解-提公因式法，熟练掌握提取公因式的方法是解本题的关键．
练习册系列答案
相关题目
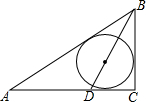如图所示的△ABC是从工厂中大量存放的铁板余料，小明测得∠C=90°，∠A的平分线分对边BC所得的两条线段分别为BD=5，DC=3，现要最大限度地利用这块余料截出一个圆形铁板．