题目内容
20.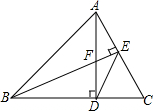 如图,AD⊥BC于D,BE⊥AC于E,AD与BE相交于点F,连接ED,图中的相似三角形的对数为( )
如图,AD⊥BC于D,BE⊥AC于E,AD与BE相交于点F,连接ED,图中的相似三角形的对数为( )| A. | 4对 | B. | 6对 | C. | 8对 | D. | 9对 |
分析 利用有两组角对应相等的两个三角形相似可判定△FAE∽△CBE∽△FBD∽△CAD,再根据圆周角定理得到点A、B、D、E四点共圆,则∠BAD=∠BED,于是可判定△ABF∽△EDF,利用∠DEC=∠ABC可判定△CDE∽△CAB.
解答 解:∵AD⊥BC于D,BE⊥AC于E,
∴∠ADC=∠AEC=90°,
∴△FAE∽△CAD,△FBD∽△CBE,
而∠ACD=∠BCE,
∴△CAD∽△CBE,
∴△FAE∽△CBE,△FAE∽△FBD,△FBD∽△CAD,
∵∠AEB=∠ADB,
∴点E、点D在以AB为直角的圆上,
即点A、B、D、E四点共圆,
∴∠BAD=∠BED,
∴△ABF∽△EDF,
∵∠DEC=∠ABC,
∴△CDE∽△CAB,
故选C.
点评 本题考查了相似三角形的判定:两组对应边的比相等且夹角对应相等的两个三角形相似;有两组角对应相等的两个三角形相似.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
10.在Rt△ABC中,∠C=90°,C为斜边,a,b为直角边,a+b=14,c=10,则Rt△ABC面积为( )
| A. | 24 | B. | 36 | C. | 48 | D. | 60 |
11. 如图,下列条件中,能判定AB∥CD的是( )
如图,下列条件中,能判定AB∥CD的是( )
 如图,下列条件中,能判定AB∥CD的是( )
如图,下列条件中,能判定AB∥CD的是( )| A. | ∠1=∠2 | B. | ∠4=∠6 | C. | ∠4=∠5 | D. | ∠1+∠3=180° |
9.若a-b=2,则a2-b2-4b的值为( )
| A. | 2 | B. | -2 | C. | 4 | D. | -4 |
10. 如图所示,点A(-1,m),B(3,n)在一次函数y=kx+b的图象上,则( )
如图所示,点A(-1,m),B(3,n)在一次函数y=kx+b的图象上,则( )
 如图所示,点A(-1,m),B(3,n)在一次函数y=kx+b的图象上,则( )
如图所示,点A(-1,m),B(3,n)在一次函数y=kx+b的图象上,则( )| A. | m=n | B. | m>n | ||
| C. | m<n | D. | m、n的大小关系不确定 |