��Ŀ����
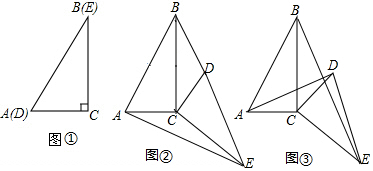
8����������ȫ��ͬ��һ����Ϊ30���ֱ�����ǰ��غ���һ����ͼ1���ã�����ABC�̶����á�DEC��ֱ�Ƕ���C��תһ���Ƕȣ������ǰ�Ķ�ֱ�DZ�AC�ij���Ϊ1����λ������������⣺
��1������DEC��ת��ͼ2��λ��ʱ���������Ӷ�Ӧ����õ���BDC�͡�AEC��д����BDC�͡�AEC�������������ϵ����֤����Ľ��ۣ�
��2����ͼ3������������Ӧ����õ���ACD�͡�BCE����֤��S��BCE=3S��ACD��
��3����ͼ2������ת��Ϊ������0��ܦ���180��ʱ��ֱ��д����Ϊ����ʱ��AE+BD��С����Сֵ�Ƕ��٣�
���� ��1�����ۣ����BDC������͡�AEC�������ȣ���ͼ���У���DM��BC��M��AN��EC��N���ɡ�ACN�ա�DCM��AAS�����Ƴ�AN=DM���ɴ˼���֤����
��2��ֻҪ֤����ACD�ס�BCE����$\frac{{S}_{��ACD}}{{S}_{��BCE}}$=��$\frac{CD}{EC}$��2=$\frac{1}{3}$������֤����
��3������ת��Ϊ90��ʱ����D���߶�BC��ʱ��AE+BD��С����Сֵ=2$\sqrt{3}$��
��� ��1���⣺���ۣ����BDC������͡�AEC�������ȣ���ͼ���У�
��DM��BC��M��AN��EC��N��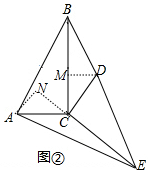
�ߡ�DEC���ɡ�ABC�Ƶ�C��ת�õ���
��BC=CE��AC=CD��
�ߡ�ACN+��BCN=90�㣬��DCM+��BCN=180��-90��=90�㣬
���ACN=��DCM��
�ڡ�ACN�͡�DCM�У�
$\left\{\begin{array}{l}{��ACN=��DCM}\\{��CMD=��N=90��}\\{AC=CD}\end{array}\right.$��
���ACN�ա�DCM��AAS����
��AN=DM��
���BDC������͡�AEC�������ȣ��ȵȸߵ������ε������ȣ���
��2��֤������ͼ���У�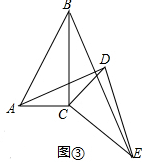
�ߡ�ACB=��DCE=90�㣬
���ACD=��BCE��
��$\frac{BC}{AC}$=$\frac{EC}{CD}$=$\sqrt{3}$��
���ACD�ס�BCE��
��$\frac{{S}_{��ACD}}{{S}_{��BCE}}$=��$\frac{CD}{EC}$��2=$\frac{1}{3}$��
��S��BCE=3S��ACD��
��3������ת��Ϊ90��ʱ����D���߶�BC��ʱ��AE+BD��С����Сֵ=2$\sqrt{3}$��
���� ���⿼����ȫ�������ε��ж������ʣ������ε�������ȱ������ε��ж������ʣ�ֱ��������30������Ե�ֱ�DZߵ���б�ߵ�һ������ʣ��������յȵȸߵ������ε������ȣ��Լ�ȫ�������ε��������ǽ���Ĺؼ���ѧ����������λ�ý��ʵ�����⣬�����п��������ͣ�

| A�� | ��a2��3=a5 | B�� | ��15x2y-10xy2����5xy=3x-2y | ||
| C�� | 10ab3�£�-5ab��=-2ab2 | D�� | a-2b3•��a2b-1��-2=$\frac{{b}^{6}}{{a}^{6}}$ |
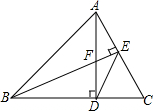 ��ͼ��AD��BC��D��BE��AC��E��AD��BE�ཻ�ڵ�F������ED��ͼ�е����������εĶ���Ϊ��������
��ͼ��AD��BC��D��BE��AC��E��AD��BE�ཻ�ڵ�F������ED��ͼ�е����������εĶ���Ϊ��������| A�� | 4�� | B�� | 6�� | C�� | 8�� | D�� | 9�� |
| A�� | ��ԭ����������ƽ��������λ | B�� | ��ԭ����������ƽ��������λ | ||
| C�� | ����x��Գ� | D�� | ����y��Գ� |

 ��ͼ����DΪ����ֱ�ǡ�ABC��һ�㣬��ACB=90�㣬��CAD=��CBD=15�㣬EΪAD�ӳ�����һ�㣬��CE=CA���������½��ۣ���DEƽ�֡�BDC�� �ڡ�BCE�ǵȱ������Σ��ۡ�AEB=45�㣻��DE=AD+CD����ȷ�Ľ����Т٢ڢۢܣ���������ţ�
��ͼ����DΪ����ֱ�ǡ�ABC��һ�㣬��ACB=90�㣬��CAD=��CBD=15�㣬EΪAD�ӳ�����һ�㣬��CE=CA���������½��ۣ���DEƽ�֡�BDC�� �ڡ�BCE�ǵȱ������Σ��ۡ�AEB=45�㣻��DE=AD+CD����ȷ�Ľ����Т٢ڢۢܣ���������ţ�