题目内容
15.计算.(1)($\frac{{a}^{2}b}{-c}$)3•($\frac{{c}^{2}}{-ab}$)2÷($\frac{bc}{a}$)4
(2)$\frac{1}{{{x^2}-4x+4}}$-$\frac{x}{{{x^2}-4}}$+$\frac{1}{2x+4}$.
分析 (1)先计算乘方,再乘除;
(2)先将分母分解因式,再通分,分母不变,分子相加减.
解答 解:(1)($\frac{{a}^{2}b}{-c}$)3•($\frac{{c}^{2}}{-ab}$)2÷($\frac{bc}{a}$)4,
=-$\frac{{a}^{6}{b}^{3}}{{c}^{3}}$$•\frac{{c}^{4}}{{a}^{2}{b}^{2}}$÷$\frac{{b}^{4}{c}^{4}}{{a}^{4}}$,
=-$\frac{{a}^{4}cb}{1}$•$\frac{{a}^{4}}{{b}^{4}{c}^{4}}$,
=-$\frac{{a}^{8}}{{b}^{3}{c}^{3}}$;
(2)$\frac{1}{{{x^2}-4x+4}}$-$\frac{x}{{{x^2}-4}}$+$\frac{1}{2x+4}$,
=$\frac{1}{(x-2)^{2}}$-$\frac{x}{(x+2)(x-2)}$+$\frac{1}{2(x+2)}$,
=$\frac{2(x+2)-2x(x-2)+(x-2)^{2}}{2(x+2)(x-2)^{2}}$,
=$\frac{-{x}^{2}+2x+8}{2(x+2)(x-2)^{2}}$,
=$\frac{-(x+2)(x-4)}{2(x+2)(x-2)^{2}}$,
=$\frac{4-x}{2(x-2)^{2}}$.
点评 本题考查了分式的混合运算,解答本题的关键在于熟练掌握分式混合运算的运算法则.

练习册系列答案
相关题目
10.在下面四个立体图形中,从左面看与从正面看所得到的平面图形不相同的是( )
| A. |  正方体 | B. |  长方体 | C. |  球 | D. |  圆锥 |
20.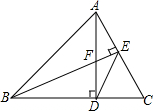 如图,AD⊥BC于D,BE⊥AC于E,AD与BE相交于点F,连接ED,图中的相似三角形的对数为( )
如图,AD⊥BC于D,BE⊥AC于E,AD与BE相交于点F,连接ED,图中的相似三角形的对数为( )
 如图,AD⊥BC于D,BE⊥AC于E,AD与BE相交于点F,连接ED,图中的相似三角形的对数为( )
如图,AD⊥BC于D,BE⊥AC于E,AD与BE相交于点F,连接ED,图中的相似三角形的对数为( )| A. | 4对 | B. | 6对 | C. | 8对 | D. | 9对 |
 如图,已知以△ABC的BC边上一点O为圆心的圆,经过A,B两点,且与BC边交于点E,D为弧BE的中点,连接AD交OE于点F,若AC=FC
如图,已知以△ABC的BC边上一点O为圆心的圆,经过A,B两点,且与BC边交于点E,D为弧BE的中点,连接AD交OE于点F,若AC=FC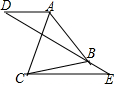 如图,直线DE过等边△ABC的顶点B,连接AD、CE,AD∥CE,∠E=30°,若BE:AD=1:$\sqrt{3}$,CE=4$\sqrt{3}$时,则BC=2$\sqrt{7}$.
如图,直线DE过等边△ABC的顶点B,连接AD、CE,AD∥CE,∠E=30°,若BE:AD=1:$\sqrt{3}$,CE=4$\sqrt{3}$时,则BC=2$\sqrt{7}$. 随着互联网的发展,同学们的学习习惯也有了改变,一些在做题遇到困难时,喜欢上网查找答案,针对这个问题,某校调查了部分学生对这种做法的意见(分为:赞成、无所谓、反对),并将调查结果绘制成图1和图2两个不完整的统计图,请根据图中提供的信息,解答下列问题:
随着互联网的发展,同学们的学习习惯也有了改变,一些在做题遇到困难时,喜欢上网查找答案,针对这个问题,某校调查了部分学生对这种做法的意见(分为:赞成、无所谓、反对),并将调查结果绘制成图1和图2两个不完整的统计图,请根据图中提供的信息,解答下列问题: