题目内容
10.在Rt△ABC中,∠C=90°,C为斜边,a,b为直角边,a+b=14,c=10,则Rt△ABC面积为( )| A. | 24 | B. | 36 | C. | 48 | D. | 60 |
分析 利用勾股定理列出关系式,再利用完全平方公式变形,将a+b与c的值代入求出ab的值,即可确定出直角三角形的面积.
解答 解:∵Rt△ABC中,∠C=90°,a+b=14,c=10,
∴由勾股定理得:a2+b2=c2,即(a+b)2-2ab=c2=100,
∴196-2ab=100,即ab=48,
则Rt△ABC的面积为$\frac{1}{2}$ab=24.
故选:A.
点评 此题考查了勾股定理,熟练掌握勾股定理是解本题的关键.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
19.下列计算正确的是( )
| A. | (a2)3=a5 | B. | (15x2y-10xy2)÷5xy=3x-2y | ||
| C. | 10ab3÷(-5ab)=-2ab2 | D. | a-2b3•(a2b-1)-2=$\frac{{b}^{6}}{{a}^{6}}$ |
20.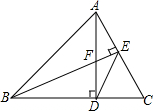 如图,AD⊥BC于D,BE⊥AC于E,AD与BE相交于点F,连接ED,图中的相似三角形的对数为( )
如图,AD⊥BC于D,BE⊥AC于E,AD与BE相交于点F,连接ED,图中的相似三角形的对数为( )
 如图,AD⊥BC于D,BE⊥AC于E,AD与BE相交于点F,连接ED,图中的相似三角形的对数为( )
如图,AD⊥BC于D,BE⊥AC于E,AD与BE相交于点F,连接ED,图中的相似三角形的对数为( )| A. | 4对 | B. | 6对 | C. | 8对 | D. | 9对 |
 如图,几何体是由3个大小完全一样的正方体组成的,它的主视图是( )
如图,几何体是由3个大小完全一样的正方体组成的,它的主视图是( )



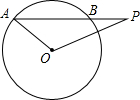 如图,已知⊙O的半径为5cm,弦AB长为8cm,P是AB延长线上一点,BP=2cm,则OP=3$\sqrt{5}$cm.
如图,已知⊙O的半径为5cm,弦AB长为8cm,P是AB延长线上一点,BP=2cm,则OP=3$\sqrt{5}$cm.