题目内容
5.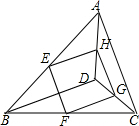 如图,E,F,G,H分别是边AB,BC,CD,DA的中点.
如图,E,F,G,H分别是边AB,BC,CD,DA的中点.(1)判断四边形EFGH的形状,并证明你的结论;
(2)当BD,AC满足什么条件时,四边形EFGH是正方形.(不要求证明)
分析 (1)在△ABC中,E、F分别是边AB、BC中点,得到EF∥AC,且EF=$\frac{1}{2}$AC,GH∥AC,且GH=$\frac{1}{2}$AC,得到四边形EFGH是平行四边形;
(2)四边形EFGH是平行四边形,再由AC=BD,得出EH=EF,从而证得四边形EFGH是菱形.对角线相等,推知四边形EFGH是正方形;
解答 解:(1)在△ABC中,E、F分别是边AB、BC中点,
所以EF∥AC,且EF=$\frac{1}{2}$AC,
同理有GH∥AC,且GH=$\frac{1}{2}$AC,
∴EF∥GH且EF=GH,
故四边形EFGH是平行四边形.
(2)EH∥BD且EH=$\frac{1}{2}$BD,
若AC=BD,则有EH=EF,
又因为四边形EFGH是平行四边形,
∴四边形EFGH是菱形,
∵AC⊥BD,
∴∠EHG=90°,
即:当AC=BD且AC⊥BD时,四边形EFGH是正方形.
点评 本题考查了三角形的中位线定理、菱形的判定及性质、平行四边形的判定及性质以及正方形的判定,中位线是三角形中的一条重要线段,由于它的性质与线段的中点及平行线紧密相连,因此,它在几何图形的计算及证明中有着广泛的应用.

练习册系列答案
 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
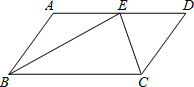 如图,在平行四边形ABCD中,BE、CE分别平分∠ABC、∠BCD,E在AD上,BE=12,CE=5,则平行四边形ABCD的周长是39.
如图,在平行四边形ABCD中,BE、CE分别平分∠ABC、∠BCD,E在AD上,BE=12,CE=5,则平行四边形ABCD的周长是39.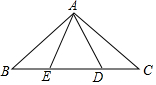 如图,在△ABC中,∠BAC=90°,AB=AC=5,点D,E在BC上,且∠DAE=45°,若CD=$\sqrt{2}$,则DE=$\frac{17\sqrt{2}}{8}$.
如图,在△ABC中,∠BAC=90°,AB=AC=5,点D,E在BC上,且∠DAE=45°,若CD=$\sqrt{2}$,则DE=$\frac{17\sqrt{2}}{8}$. 一个有进水管与出水管的容器,从某时刻开始4min内只进水不出水,在随后的8min内既进水又出水,每分钟的进水量和出水量是两个常数,容器内的水量y(单位:L)与时间(单位:min)之间的关系如图所示.
一个有进水管与出水管的容器,从某时刻开始4min内只进水不出水,在随后的8min内既进水又出水,每分钟的进水量和出水量是两个常数,容器内的水量y(单位:L)与时间(单位:min)之间的关系如图所示.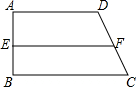 如图,在四边形ABCD中,AD∥BC,AD=4,BC=5,E、F分别为AB和DC的中点,则EF的长为$\frac{9}{2}$.
如图,在四边形ABCD中,AD∥BC,AD=4,BC=5,E、F分别为AB和DC的中点,则EF的长为$\frac{9}{2}$.