题目内容
17.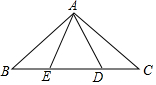 如图,在△ABC中,∠BAC=90°,AB=AC=5,点D,E在BC上,且∠DAE=45°,若CD=$\sqrt{2}$,则DE=$\frac{17\sqrt{2}}{8}$.
如图,在△ABC中,∠BAC=90°,AB=AC=5,点D,E在BC上,且∠DAE=45°,若CD=$\sqrt{2}$,则DE=$\frac{17\sqrt{2}}{8}$.
分析 根据等腰直角三角形的性质得∠2=∠C=45°,再把△ACD绕点A顺时针旋转90°得到△ABF,如图,根据旋转的性质得∠1=∠C=45°,BF=CD,AF=AD,∠BAF=∠CAD,∠DAF=90°,接着证明∠EAD=∠EAF,然后根据“SAS”可判断△ADE≌△ADF,得到DE=FE;由于∠FBE=∠1+∠2=90°,根据勾股定理得BE2+BF2=EF2,推出CD2+BE2=DE2,由此即可解决问题.
解答 证明:∵∠BAC=90°,AB=AC,
∴∠2=∠C=45°,
把△ACD绕点A顺时针旋转90°得到△ABF,如图,则∠1=∠C=45°,BF=CD,AF=AD,∠BAF=∠CAD,∠DAF=90°,
∵∠DAE=45°,
∴∠CAD+∠BAE=45°,
∴∠BAE+∠BAF=45°,即∠EAF=45°,
∴∠EAD=∠EAF,
在△ADE和△AFE中
$\left\{\begin{array}{l}{AE=AE}\\{∠EAD=∠EAF}\\{AD=AF}\end{array}\right.$,
∴△ADE≌△AFE,
∴DE=FE,
∵∠FBE=∠1+∠2=90°,
∴BE2+BF2=EF2,
∴CD2+BE2=DE2,
Rt△ABC中,∵AB=AC=5,
∴BC=$\sqrt{A{B}^{2}+A{C}^{2}}$=5$\sqrt{2}$,
∵CD=$\sqrt{2}$,
∴BD=4$\sqrt{2}$,设DE=x,则BE=4$\sqrt{2}$-x,
则有x2=(4$\sqrt{2}$-x)2+($\sqrt{2}$)2,
∴x=$\frac{17\sqrt{2}}{8}$,
∴ED=$\frac{17\sqrt{2}}{8}$.
点评 本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了勾股定理和等腰直角三角形的性质.

 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案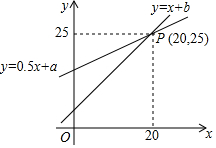 如图,一次函数y=x+b与y=0.5x+a图象交点为P(20,25).则不等式:x+b>0.5x+a的解集是( )
如图,一次函数y=x+b与y=0.5x+a图象交点为P(20,25).则不等式:x+b>0.5x+a的解集是( )| A. | x>25 | B. | x>20 | C. | x<25 | D. | x<20 |
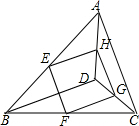 如图,E,F,G,H分别是边AB,BC,CD,DA的中点.
如图,E,F,G,H分别是边AB,BC,CD,DA的中点. 如图,将三角形ABC向右平移2个单位长度,再向下平移3个单位长度,得到对应的三角形A1B1C1.
如图,将三角形ABC向右平移2个单位长度,再向下平移3个单位长度,得到对应的三角形A1B1C1.