题目内容
14. 一个有进水管与出水管的容器,从某时刻开始4min内只进水不出水,在随后的8min内既进水又出水,每分钟的进水量和出水量是两个常数,容器内的水量y(单位:L)与时间(单位:min)之间的关系如图所示.
一个有进水管与出水管的容器,从某时刻开始4min内只进水不出水,在随后的8min内既进水又出水,每分钟的进水量和出水量是两个常数,容器内的水量y(单位:L)与时间(单位:min)之间的关系如图所示.(1)每分进水5升、出水$\frac{15}{4}$升;(直接填出答案)
(2)当4≤x≤12时,求y关于x的函数解析式.
分析 (1)每分钟的进水量根据前4分钟的图象求出,出水量根据后8分钟的水量变化求解;
(2)用待定系数法求对应的函数关系式即可.
解答 解:
(1)根据图象,每分钟进水20÷4=5升,
设每分钟出水m升,则 5×8-8m=30-20,
解得:m=$\frac{15}{4}$.
所以每分钟进水、出水各是5升、$\frac{15}{4}$升,
故答案为:5,$\frac{15}{4}$;
(2)设当4≤x≤12时的直线方程为:y=kx+b(k≠0).
∵图象过(4,20)、(12,30),
∴$\left\{\begin{array}{l}{20=4k+b}\\{30=12k+b}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=\frac{5}{4}}\\{b=15}\end{array}\right.$,
∴y=$\frac{5}{4}$x+15 (4≤x≤12).
点评 此题考查了一次函数的应用,解题时首先正确理解题意,然后根据题意利用待定系数法确定函数的解析式,接着利用函数的性质即可解决问题.

练习册系列答案
相关题目
9.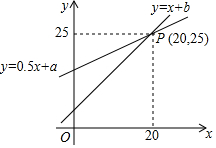 如图,一次函数y=x+b与y=0.5x+a图象交点为P(20,25).则不等式:x+b>0.5x+a的解集是( )
如图,一次函数y=x+b与y=0.5x+a图象交点为P(20,25).则不等式:x+b>0.5x+a的解集是( )
 如图,一次函数y=x+b与y=0.5x+a图象交点为P(20,25).则不等式:x+b>0.5x+a的解集是( )
如图,一次函数y=x+b与y=0.5x+a图象交点为P(20,25).则不等式:x+b>0.5x+a的解集是( )| A. | x>25 | B. | x>20 | C. | x<25 | D. | x<20 |
 画图并填空:如图,每个小正方形的边长为1个单位,每个小正方形的顶点叫格点.
画图并填空:如图,每个小正方形的边长为1个单位,每个小正方形的顶点叫格点.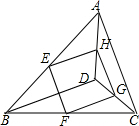 如图,E,F,G,H分别是边AB,BC,CD,DA的中点.
如图,E,F,G,H分别是边AB,BC,CD,DA的中点.
 如图,将三角形ABC向右平移2个单位长度,再向下平移3个单位长度,得到对应的三角形A1B1C1.
如图,将三角形ABC向右平移2个单位长度,再向下平移3个单位长度,得到对应的三角形A1B1C1.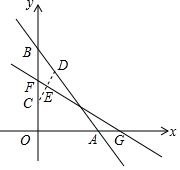 如图,直线y=-$\frac{4}{3}$x+4与x轴、y轴分别相交于点A,B,点C从点O出发沿射线OB方向以每秒1个单位速度运动,同时点D从点B出发沿BA方向以相同的速度向点A运动.当点D到达点A同时停止运动,点C也随之停止.连接CD,过CD的中点E作EF⊥CD交y轴于点F,交x轴于点G,设运动的时间时t秒.
如图,直线y=-$\frac{4}{3}$x+4与x轴、y轴分别相交于点A,B,点C从点O出发沿射线OB方向以每秒1个单位速度运动,同时点D从点B出发沿BA方向以相同的速度向点A运动.当点D到达点A同时停止运动,点C也随之停止.连接CD,过CD的中点E作EF⊥CD交y轴于点F,交x轴于点G,设运动的时间时t秒.