题目内容
4.已知一次函数y=ax+b(a、b是常数,且a≠0),x与y的部分对应值如表:| x | -2 | -1 | 0 | 1 | 2 | 3 |
| y | 6 | 4 | 2 | 0 | -2 | -4 |
(2)你还有更好的方法吗?说出来和大家分享.
分析 (1)将(0,2),(1,0)两点的坐标代入y=ax+b,求出一次函数的解析式,再根据一次函数的性质画出函数y=ax+b的图象,观察图象得出与x轴的交点坐标,那么方程ax+b=0的解是直线与x轴交点横坐标的值;
(2)观察表格中y=0时x的对应值即为方程ax+b=0的解.
解答 解:(1)将(0,2),(1,0)代入y=ax+b,
得$\left\{\begin{array}{l}{b=2}\\{a+b=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{a=-2}\\{b=2}\end{array}\right.$,
所以一次函数的解析式为y=-2x+2,
函数y=-2x+2的图象如下所示,
由图可知,该图象与x轴交于点(1,0),
所以方程ax+b=0的解是x=1;
(2)观察表格,可知y=0时,x=1,所以方程ax+b=0的解为x=1.
故答案为y=-2x+2;y=-2x+2;(1,0);x=1.
点评 本题考查了一次函数与一元一次方程,一次函数y=ax+b的图象与x轴交点的横坐标的值即为方程ax+b=0的解.也考查了待定系数法求一次函数的解析式,一次函数的图象与性质.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
15.已知a是非零实数,则下列不等式一定成立的有( )
a2+1>1,1-a2<0,1+$\frac{1}{a}$>1,|a+$\frac{1}{a}$|≥2,|a-1|≤|a|+1.
a2+1>1,1-a2<0,1+$\frac{1}{a}$>1,|a+$\frac{1}{a}$|≥2,|a-1|≤|a|+1.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
14.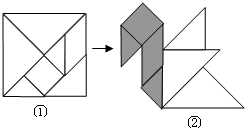 用正方形纸板制成一副七巧板,如图①,将它拼成“小天鹅”图案,如图②,若其中阴影部分的面积为6,则正方形纸板的面积为( )
用正方形纸板制成一副七巧板,如图①,将它拼成“小天鹅”图案,如图②,若其中阴影部分的面积为6,则正方形纸板的面积为( )
 用正方形纸板制成一副七巧板,如图①,将它拼成“小天鹅”图案,如图②,若其中阴影部分的面积为6,则正方形纸板的面积为( )
用正方形纸板制成一副七巧板,如图①,将它拼成“小天鹅”图案,如图②,若其中阴影部分的面积为6,则正方形纸板的面积为( )| A. | 12 | B. | 16 | C. | 18 | D. | 25 |
15.已知,△ABC∽△DEF,△ABC与△DEF的面积之比为1:2,当BC=1,对应边EF的长是( )
| A. | $\sqrt{2}$ | B. | 2 | C. | 3 | D. | 4 |