题目内容
15.已知,△ABC∽△DEF,△ABC与△DEF的面积之比为1:2,当BC=1,对应边EF的长是( )| A. | $\sqrt{2}$ | B. | 2 | C. | 3 | D. | 4 |
分析 根据相似三角形面积的比等于相似比的平方列出比例式,代入数值计算即可得解.
解答 解:∵△ABC∽△DEF,△ABC与△DEF的面积之比为1:2,
∴(BC:EF)2=1:2,
解得BC:EF=1:$\sqrt{2}$,
∵BC=1,
∴EF=$\sqrt{2}$.
故选A.
点评 本题考查了相似三角形的性质,主要利用了相似三角形面积的比等于相似比的平方,比较简单,熟记性质是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
4.已知一次函数y=ax+b(a、b是常数,且a≠0),x与y的部分对应值如表:
(1)牟宗华同学先用待定系数法求出函数y=ax+b的表达式是y=-2x+2,再画出函数y=-2x+2的图象,该图象与x轴交于点(1,0),所有方程ax+b=0的解是x=1;
(2)你还有更好的方法吗?说出来和大家分享.
| x | -2 | -1 | 0 | 1 | 2 | 3 |
| y | 6 | 4 | 2 | 0 | -2 | -4 |
(2)你还有更好的方法吗?说出来和大家分享.
6.10的平方根是( )
| A. | ±$\sqrt{10}$ | B. | ±$\sqrt{5}$ | C. | ±5 | D. | 5 |
3. 如图,AB∥CD,∠C=32°,∠E=48°,则∠B的度数为( )
如图,AB∥CD,∠C=32°,∠E=48°,则∠B的度数为( )
 如图,AB∥CD,∠C=32°,∠E=48°,则∠B的度数为( )
如图,AB∥CD,∠C=32°,∠E=48°,则∠B的度数为( )| A. | 120° | B. | 128° | C. | 110° | D. | 100° |
10.下列图形中,既是轴对称图形又是中心对称图形的有( )


| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
20.关于二次函数y=-(x+1)2+2的图象,下列判断正确的是( )
| A. | 图象开口向上 | B. | 图象的对称轴是直线x=1 | ||
| C. | 图象有最低点 | D. | 图象的顶点坐标为(-1,2) |
5.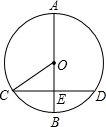 如图,已知AB是⊙O的直径,弦CD⊥AB于点E,若AB=6cm,CD=4cm,则sin∠OCE等于( )
如图,已知AB是⊙O的直径,弦CD⊥AB于点E,若AB=6cm,CD=4cm,则sin∠OCE等于( )
 如图,已知AB是⊙O的直径,弦CD⊥AB于点E,若AB=6cm,CD=4cm,则sin∠OCE等于( )
如图,已知AB是⊙O的直径,弦CD⊥AB于点E,若AB=6cm,CD=4cm,则sin∠OCE等于( )| A. | $\frac{2}{3}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{5}}{2}$ | D. | $\frac{\sqrt{5}}{3}$ |
 某城区为了改善全区中、小学办学条件,去年分三批为学校配备了教学器材,其中第三批共投入经费144000元.采购了电子白板16块和投影机8台.已知1块电子白板的单价比1台投影机的多3000元.
某城区为了改善全区中、小学办学条件,去年分三批为学校配备了教学器材,其中第三批共投入经费144000元.采购了电子白板16块和投影机8台.已知1块电子白板的单价比1台投影机的多3000元.