题目内容
2.甲、乙两人加工一批零件,甲完成120个与乙完成100个所用的时间相同.已知甲比乙每天多完成4个.设甲每天完成x个零件,依题意列方程$\frac{120}{x}$=$\frac{100}{x-4}$.分析 设甲每天完成x个零件,则乙每天完成(x-4)个零件,根据“甲完成120个所用时间=乙完成100个所用的时间”列出方程即可.
解答 解:设甲每天完成x个零件,则乙每天完成(x-4)个零件,
根据题意,得:$\frac{120}{x}$=$\frac{100}{x-4}$,
故答案为:$\frac{120}{x}$=$\frac{100}{x-4}$.
点评 本题主要考查由实际问题抽象出分式方程,解题的关键是确定题目中蕴含的相等关系.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
10.若关于x的一元一次不等式组$\left\{\begin{array}{l}{x-2k≤0}\\{x+k>2}\end{array}\right.$有解,则k的取值范围为( )
| A. | k>-$\frac{2}{3}$ | B. | k>$\frac{2}{3}$ | C. | k≤$\frac{2}{3}$ | D. | k≥-$\frac{2}{3}$ |
10.若二次函数y=ax2+bx+c(a≠0)的图象经过点A(1,0),B(0,1),且顶点在第四象限,则s=4a+2b+c的取值范围是( )
| A. | s>-1且s≠1 | B. | s>-3且s≠1 | C. | -3<s<-1 | D. | -1<s<0 |
12.化化工产品C是由A,B两种原料加工而成的,每个C产品的质量为50kg,经测定加工费与A的质量的平方成正比例;A原料的成本10元/kg,B原料的成本:40元/kg;这种C产品中A的含量不能低于10%,又不能高于60%;C产品的出厂价经核算是含B的质量的一次函数.经市场调查,当含A的质量不高于8kg时:利润=出厂价-成本;当含A的质量不低于8kg时,每个C产品的利润将与含A的质量成反比例.
下表是每个C产品的成本及出厂价一览表的一部分.
(1)求出每个C产品的成本y(元)与含A的质量x(kg)之间的函数关系式,并写出x的范围;(每个C成本=A的成本+B的成本+加工费用);
(2)求出每个C产品的利润w(元)与含A的质量x(kg)之间的函数关系式.
下表是每个C产品的成本及出厂价一览表的一部分.
| 含A:10% | 含A(30%) | |
| 成本(元/个) | 1875 | 1775 |
| 出厂价 | 2450 | 2350 |
(2)求出每个C产品的利润w(元)与含A的质量x(kg)之间的函数关系式.
 如图,一次函数y=kx+2k(k>0)的图象交x轴于点A,P为该一次函数在第一象限内图象上一点,点C(m,n)与点P关于y轴对称,且满足n-m=6,若△APC是直角三角形,则k的值为1.
如图,一次函数y=kx+2k(k>0)的图象交x轴于点A,P为该一次函数在第一象限内图象上一点,点C(m,n)与点P关于y轴对称,且满足n-m=6,若△APC是直角三角形,则k的值为1.



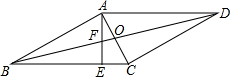 如图,在平行四边形ABCD中,对角线AC、BD交于点O、AC⊥AB、∠ABC=30°,过点A作AE⊥BC于点E,交BD于点F,则$\frac{AF}{AO}$=$\frac{4\sqrt{3}}{7}$.
如图,在平行四边形ABCD中,对角线AC、BD交于点O、AC⊥AB、∠ABC=30°,过点A作AE⊥BC于点E,交BD于点F,则$\frac{AF}{AO}$=$\frac{4\sqrt{3}}{7}$.