题目内容
10.若二次函数y=ax2+bx+c(a≠0)的图象经过点A(1,0),B(0,1),且顶点在第四象限,则s=4a+2b+c的取值范围是( )| A. | s>-1且s≠1 | B. | s>-3且s≠1 | C. | -3<s<-1 | D. | -1<s<0 |
分析 把A、B的坐标代入解析式求出c=1,b=-a-1,根据对称轴得出b<0,求出a>-1,求出s>-3,即可得出答案.
解答 解:将点A(1,0),B(0,1)分别代入抛物线解析式,得c=1,b=-a-1,
∴s=4a+2b+c=4a+2(-a-1)+1=2a-1,
∵顶点在第四象限,∴对称轴x=-$\frac{b}{2a}$>0,a>0,
∴2b<0,
又由b=-a-1<0,
a>-1,
2a>-2,
2a-1>-3,
即S>-3,
当a=1时,b=0,对称轴是y轴,和已知顶点在第四象限不符,
∴S>-3且A≠1,
故选B.
点评 本题考查了二次函数的最值问题,二次函数的图象和性质,能求出a的范围是解此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.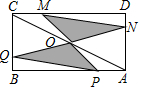 如图,矩形ABCD中,AB=8,BC=4,O为对角线AC的中点,点P,Q分别从A和B两点同时出发,在边AB和BC上匀速运动,并且同时到达终点B,C,连接PO,QO并延长分别与CD,DA交于点M,N,在整个运动过程中,图中阴影部分面积的大小变化情况是( )
如图,矩形ABCD中,AB=8,BC=4,O为对角线AC的中点,点P,Q分别从A和B两点同时出发,在边AB和BC上匀速运动,并且同时到达终点B,C,连接PO,QO并延长分别与CD,DA交于点M,N,在整个运动过程中,图中阴影部分面积的大小变化情况是( )
 如图,矩形ABCD中,AB=8,BC=4,O为对角线AC的中点,点P,Q分别从A和B两点同时出发,在边AB和BC上匀速运动,并且同时到达终点B,C,连接PO,QO并延长分别与CD,DA交于点M,N,在整个运动过程中,图中阴影部分面积的大小变化情况是( )
如图,矩形ABCD中,AB=8,BC=4,O为对角线AC的中点,点P,Q分别从A和B两点同时出发,在边AB和BC上匀速运动,并且同时到达终点B,C,连接PO,QO并延长分别与CD,DA交于点M,N,在整个运动过程中,图中阴影部分面积的大小变化情况是( )| A. | 一直增大 | B. | 一直减小 | C. | 先减小后增大 | D. | 先增大后减小 |
19.5月14-15日“一带一路”论坛峰会在北京隆重召开,促进了我国与世界各国的互联互通互惠,“一带一路”地区覆盖总人数约为44亿人,44亿这个数用科学记数法表示为( )
| A. | 4.4×108 | B. | 4.4×109 | C. | 4×109 | D. | 44×108 |
16.点A(1,y1)、B(3,y2)是反比例函数y=$\frac{9}{x}$图象上的两点,则y1、y2的大小关系是( )
| A. | y1>y2 | B. | y1=y2 | C. | y1<y2 | D. | 不能确定 |
15.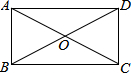 如图,矩形的两条对角线的一个交角为60°,AC+BD=20cm,则AB的长为( )
如图,矩形的两条对角线的一个交角为60°,AC+BD=20cm,则AB的长为( )
 如图,矩形的两条对角线的一个交角为60°,AC+BD=20cm,则AB的长为( )
如图,矩形的两条对角线的一个交角为60°,AC+BD=20cm,则AB的长为( )| A. | 10cm | B. | 8cm | C. | 6cm | D. | 5cm |
20.输入一组数据,按下列程序进行计算(x+8)2-826,输出结果如表:
分析表格中的数据,估计方程(x+8)2-826=0的一个正数解x的大致范围为( )
| x | 20.5 | 20.6 | 20.7 | 20.8 | 20.9 |
| 输出 | -13.75 | -8.04 | -2.31 | 3.44 | 9.21 |
| A. | 20.5<x<20.6 | B. | 20.6<x<20.7 | C. | 20.7<x<20.8 | D. | 20.8<x<20.9 |
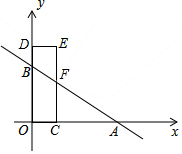 如图,在平面直角坐标系中,直线y=kx+b与x轴、y轴分别交于点A(6,0),B(0,3),点F为线段AB上任意一点,过点F作FC⊥OA于点C,延长CF至点E使EF=CF,作ED⊥y轴于点D.
如图,在平面直角坐标系中,直线y=kx+b与x轴、y轴分别交于点A(6,0),B(0,3),点F为线段AB上任意一点,过点F作FC⊥OA于点C,延长CF至点E使EF=CF,作ED⊥y轴于点D.