题目内容
7.求二次函数y=x2-2x-3的图象与坐标轴的交点坐标、顶点坐标以及对称轴.分析 令x=0知y=-3,可得抛物线与y轴交点;令y=0求得x,可得抛物线与x轴的交点;将抛物线配方成顶点式可得其顶点坐标及对称轴.
解答 解:当x=0时,y=-3,
∴抛物线与y轴的交点为(0,-3),
当y=0时,x2-2x-3=0,
解得:x=-1或x=3,
∴抛物线与x轴的交点为(-1,0)、(3,0),
∵y=x2-2x-3=(x-1)2-4,
∴抛物线的顶点坐标为(1,-4)、对称轴为x=1.
点评 本题主要考查抛物线与坐标轴的交点及二次函数的性质,熟练掌握抛物线与坐标轴的交点坐标的求法是解题的关键.

练习册系列答案
相关题目
16.点A(1,y1)、B(3,y2)是反比例函数y=$\frac{9}{x}$图象上的两点,则y1、y2的大小关系是( )
| A. | y1>y2 | B. | y1=y2 | C. | y1<y2 | D. | 不能确定 |
15.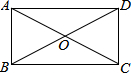 如图,矩形的两条对角线的一个交角为60°,AC+BD=20cm,则AB的长为( )
如图,矩形的两条对角线的一个交角为60°,AC+BD=20cm,则AB的长为( )
 如图,矩形的两条对角线的一个交角为60°,AC+BD=20cm,则AB的长为( )
如图,矩形的两条对角线的一个交角为60°,AC+BD=20cm,则AB的长为( )| A. | 10cm | B. | 8cm | C. | 6cm | D. | 5cm |
17.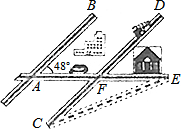 某城市几条道路的位置关系如图所示,已知AB∥CD,AE与AB的夹角为48°,若CF与EF的长度相等,则∠C的度数为( )
某城市几条道路的位置关系如图所示,已知AB∥CD,AE与AB的夹角为48°,若CF与EF的长度相等,则∠C的度数为( )
 某城市几条道路的位置关系如图所示,已知AB∥CD,AE与AB的夹角为48°,若CF与EF的长度相等,则∠C的度数为( )
某城市几条道路的位置关系如图所示,已知AB∥CD,AE与AB的夹角为48°,若CF与EF的长度相等,则∠C的度数为( )| A. | 48° | B. | 40° | C. | 30° | D. | 24° |
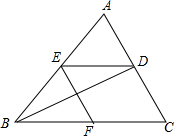 如图,已知BD是△ABC的角平分线,点E、F分别在边AB、BC上,ED∥BC,BE=CF.
如图,已知BD是△ABC的角平分线,点E、F分别在边AB、BC上,ED∥BC,BE=CF.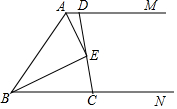 如图,AM∥BN,∠MAB和∠NBA的平分线交于E点.求:
如图,AM∥BN,∠MAB和∠NBA的平分线交于E点.求: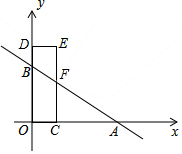 如图,在平面直角坐标系中,直线y=kx+b与x轴、y轴分别交于点A(6,0),B(0,3),点F为线段AB上任意一点,过点F作FC⊥OA于点C,延长CF至点E使EF=CF,作ED⊥y轴于点D.
如图,在平面直角坐标系中,直线y=kx+b与x轴、y轴分别交于点A(6,0),B(0,3),点F为线段AB上任意一点,过点F作FC⊥OA于点C,延长CF至点E使EF=CF,作ED⊥y轴于点D.