题目内容
17．
如图，一次函数y=kx+2k（k＞0）的图象交x轴于点A，P为该一次函数在第一象限内图象上一点，点C（m，n）与点P关于y轴对称，且满足n-m=6，若△APC是直角三角形，则k的值为1．
分析 根据一次函数图象上点的坐标特征可求出点A的坐标，由C、P关于y轴对称结合△APC为直角三角形，可以用k的代数式表示点P的坐标，然后根据n-m=6可以求得k的值，从而可以解答本题．
解答 解：∵y=kx+2k，
∴y=0时，x=-2，
∴点A的坐标为（-2，0），
∵P为该一次函数在第一象限内图象上一点，点C（m，n）与点P关于y轴对称，△APC是直角三角形，
∴点P为（-m，n），m=-2，∠ACP=90°，
当x=2时，y=kx+2k=k×2+2k=4k，
∴点P的坐标为（2，4k），
∴m=-2，n=4k，
∵n-m=6，
∴4k-（-2）=6，得k=1，
故答案为：1．
点评 本题考查一次函数图象上点的坐标特征、关于x轴、y轴对称的点的坐标，解答本题的关键是明确题意，找出所求问题需要的条件，利用数形结合的思想解答．
练习册系列答案
相关题目
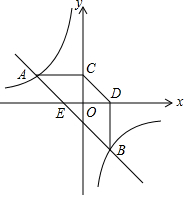如图，已知A（-4，n），B（4-n，-4）是直线y=kx+b和双曲线y=$\frac{m}{x}$的两个交点，过点A，B分别作AC⊥y轴，BD⊥x轴，垂足为C，D．
6．在△ABC中，∠A，∠B，∠C的度数之比为2：3：4，则∠B的度数为（ ）
| A． | 120° | B． | 80° | C． | 60° | D． | 40° |
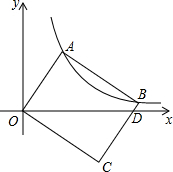如图，在平面直角坐标系xOy，矩形OABC的顶点A、B在双曲线y=$\frac{k}{x}$（x＞0）上．若点A的坐标为（1，2），则点B坐标为（4，$\frac{1}{2}$）．
9．
将一副三角板如图所示放置，且满足BC∥DE，则∠AFC=（ ）
将一副三角板如图所示放置，且满足BC∥DE，则∠AFC=（ ）| A． | 80° | B． | 75° | C． | 70° | D． | 65° |
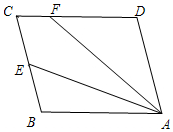如图，平行四边形ABCD中，E是BC边的中点，连接AE、F为CD边上一点，且满足∠DFA=2∠BAE．