题目内容
11.已知二次函数的表达式为y=x2+mx+n.(1)若这个二次函数的图象与x轴交于点A(1,0),点B(3,0),求实数m,n的值;
(2)若△ABC是有一个内角为30°的直角三角形,∠C为直角,sinA,cosB是方程x2+mx+n=0的两个根,求实数m,n的值.
分析 (1)根据点A、B的坐标,利用待定系数法即可求出m、n的值;
(2)分∠A=30°或∠B=30°两种情况考虑:当∠A=30°时,求出sinA、cosB的值,利用根与系数的关系即可求出m、n的值;当∠B=30°时,求出sinA、cosB的值,利用根与系数的关系即可求出m、n的值.
解答 解:(1)将A(1,0)、B(3,0)代入y=x2+mx+n中,
$\left\{\begin{array}{l}{1+m+n=0}\\{9+3m+n=0}\end{array}\right.$,解得:$\left\{\begin{array}{l}{m=-4}\\{n=3}\end{array}\right.$,
∴实数m=-4、n=3.
(2)当∠A=30°时,sinA=cosB=$\frac{1}{2}$,
∴-m=$\frac{1}{2}$+$\frac{1}{2}$,n=$\frac{1}{2}$×$\frac{1}{2}$,
∴m=-1,n=$\frac{1}{4}$;
当∠B=30°时,sinA=cosB=$\frac{\sqrt{3}}{2}$,
∴-m=$\frac{\sqrt{3}}{2}$+$\frac{\sqrt{3}}{2}$,n=$\frac{\sqrt{3}}{2}$×$\frac{\sqrt{3}}{2}$,
∴m=-$\sqrt{3}$,n=$\frac{3}{4}$.
综上所述:m=-1、n=$\frac{1}{4}$或m=-$\sqrt{3}$、n=$\frac{3}{4}$.
点评 本题考查了抛物线与x轴的交点、待定系数法求二次函数解析式、解直角三角形以及根与系数的关系,解题的关键是:(1)根据点的坐标,利用待定系数法求出m、n的值;(2)分∠A=30°或∠B=30°两种情况,求出m、n的值.

 阅读快车系列答案
阅读快车系列答案| A. | 4.4×108 | B. | 4.4×109 | C. | 4×109 | D. | 44×108 |
| A. | 120° | B. | 80° | C. | 60° | D. | 40° |
| A. | y1>y2 | B. | y1=y2 | C. | y1<y2 | D. | 不能确定 |
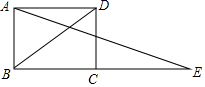 如图,BD为矩形ABCD的一条对角线,延长BC至E,使CE=BD,连接AE.若AB=1,∠AEB=15°,求BD的长度.
如图,BD为矩形ABCD的一条对角线,延长BC至E,使CE=BD,连接AE.若AB=1,∠AEB=15°,求BD的长度.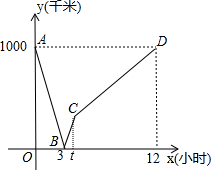 首条贯通丝绸之路经济带的高铁线--宝兰客专进入全线拉通试验阶段.宝兰客专的通车对加快西北地区与“一带一路”沿线国家和地区的经贸合作、人文交流具有十分重要的意义.试运行期间,一列动车从西安开往西宁,一列普通列车从西宁开往西安,两车同时出发,设普通列车行驶的时间为x(小时),两车之间的距离为y(千米),图中的折线表示y与x之间的函数关系,根据图象进行以下探究:
首条贯通丝绸之路经济带的高铁线--宝兰客专进入全线拉通试验阶段.宝兰客专的通车对加快西北地区与“一带一路”沿线国家和地区的经贸合作、人文交流具有十分重要的意义.试运行期间,一列动车从西安开往西宁,一列普通列车从西宁开往西安,两车同时出发,设普通列车行驶的时间为x(小时),两车之间的距离为y(千米),图中的折线表示y与x之间的函数关系,根据图象进行以下探究: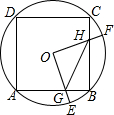 如图,边长为2的正方形ABCD内接于⊙O,点E是$\widehat{AB}$上一点(不与A、B重合),点F是$\widehat{BC}$上一点,连接OE,OF,分别与AB,BC交于点G,H,有下列结论:
如图,边长为2的正方形ABCD内接于⊙O,点E是$\widehat{AB}$上一点(不与A、B重合),点F是$\widehat{BC}$上一点,连接OE,OF,分别与AB,BC交于点G,H,有下列结论: