题目内容
10.若关于x的一元一次不等式组$\left\{\begin{array}{l}{x-2k≤0}\\{x+k>2}\end{array}\right.$有解,则k的取值范围为( )| A. | k>-$\frac{2}{3}$ | B. | k>$\frac{2}{3}$ | C. | k≤$\frac{2}{3}$ | D. | k≥-$\frac{2}{3}$ |
分析 先分别解两个不等式得到x≤2k和x>2-k,利用大小小大中间找得到2-k<2k,然后解关于k的一元一次不等式即可.
解答 解:$\left\{\begin{array}{l}{x-2k≤0①}\\{x+k>2②}\end{array}\right.$,
解①得x≤2k,
解②得x>2-k,
因为不等式组$\left\{\begin{array}{l}{x-2k≤0}\\{x+k>2}\end{array}\right.$有解,
所以2-k<2k,
解得k>$\frac{2}{3}$.
故选B.
点评 本题考查了解一元一次不等式组:解一元一次不等式组时,一般先求出其中各不等式的解集,再求出这些解集的公共部分,利用数轴可以直观地表示不等式组的解集.
方法与步骤:①求不等式组中每个不等式的解集;②利用数轴求公共部分.解集的规律:同大取大;同小取小;大小小大中间找;大大小小找不到.

练习册系列答案
相关题目
20. 如图,在矩形ABCD中,已知AB=4,BC=3,矩形在直线上绕其右下角的顶点B向右旋转90°至图①位置,再绕右下角的顶点继续向右旋转90°至图②位置,…,以此类推,这样连续旋转2017次后,顶点A在整个旋转过程中所经过的路程之和是( )
如图,在矩形ABCD中,已知AB=4,BC=3,矩形在直线上绕其右下角的顶点B向右旋转90°至图①位置,再绕右下角的顶点继续向右旋转90°至图②位置,…,以此类推,这样连续旋转2017次后,顶点A在整个旋转过程中所经过的路程之和是( )
 如图,在矩形ABCD中,已知AB=4,BC=3,矩形在直线上绕其右下角的顶点B向右旋转90°至图①位置,再绕右下角的顶点继续向右旋转90°至图②位置,…,以此类推,这样连续旋转2017次后,顶点A在整个旋转过程中所经过的路程之和是( )
如图,在矩形ABCD中,已知AB=4,BC=3,矩形在直线上绕其右下角的顶点B向右旋转90°至图①位置,再绕右下角的顶点继续向右旋转90°至图②位置,…,以此类推,这样连续旋转2017次后,顶点A在整个旋转过程中所经过的路程之和是( )| A. | 3022.5π | B. | 3024π | C. | 3025.5π | D. | 3026π |
18.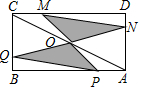 如图,矩形ABCD中,AB=8,BC=4,O为对角线AC的中点,点P,Q分别从A和B两点同时出发,在边AB和BC上匀速运动,并且同时到达终点B,C,连接PO,QO并延长分别与CD,DA交于点M,N,在整个运动过程中,图中阴影部分面积的大小变化情况是( )
如图,矩形ABCD中,AB=8,BC=4,O为对角线AC的中点,点P,Q分别从A和B两点同时出发,在边AB和BC上匀速运动,并且同时到达终点B,C,连接PO,QO并延长分别与CD,DA交于点M,N,在整个运动过程中,图中阴影部分面积的大小变化情况是( )
 如图,矩形ABCD中,AB=8,BC=4,O为对角线AC的中点,点P,Q分别从A和B两点同时出发,在边AB和BC上匀速运动,并且同时到达终点B,C,连接PO,QO并延长分别与CD,DA交于点M,N,在整个运动过程中,图中阴影部分面积的大小变化情况是( )
如图,矩形ABCD中,AB=8,BC=4,O为对角线AC的中点,点P,Q分别从A和B两点同时出发,在边AB和BC上匀速运动,并且同时到达终点B,C,连接PO,QO并延长分别与CD,DA交于点M,N,在整个运动过程中,图中阴影部分面积的大小变化情况是( )| A. | 一直增大 | B. | 一直减小 | C. | 先减小后增大 | D. | 先增大后减小 |
19.5月14-15日“一带一路”论坛峰会在北京隆重召开,促进了我国与世界各国的互联互通互惠,“一带一路”地区覆盖总人数约为44亿人,44亿这个数用科学记数法表示为( )
| A. | 4.4×108 | B. | 4.4×109 | C. | 4×109 | D. | 44×108 |
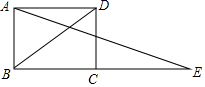 如图,BD为矩形ABCD的一条对角线,延长BC至E,使CE=BD,连接AE.若AB=1,∠AEB=15°,求BD的长度.
如图,BD为矩形ABCD的一条对角线,延长BC至E,使CE=BD,连接AE.若AB=1,∠AEB=15°,求BD的长度.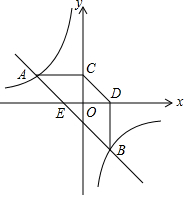 如图,已知A(-4,n),B(4-n,-4)是直线y=kx+b和双曲线y=$\frac{m}{x}$的两个交点,过点A,B分别作AC⊥y轴,BD⊥x轴,垂足为C,D.
如图,已知A(-4,n),B(4-n,-4)是直线y=kx+b和双曲线y=$\frac{m}{x}$的两个交点,过点A,B分别作AC⊥y轴,BD⊥x轴,垂足为C,D.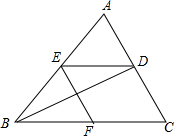 如图,已知BD是△ABC的角平分线,点E、F分别在边AB、BC上,ED∥BC,BE=CF.
如图,已知BD是△ABC的角平分线,点E、F分别在边AB、BC上,ED∥BC,BE=CF.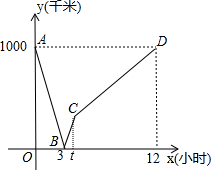 首条贯通丝绸之路经济带的高铁线--宝兰客专进入全线拉通试验阶段.宝兰客专的通车对加快西北地区与“一带一路”沿线国家和地区的经贸合作、人文交流具有十分重要的意义.试运行期间,一列动车从西安开往西宁,一列普通列车从西宁开往西安,两车同时出发,设普通列车行驶的时间为x(小时),两车之间的距离为y(千米),图中的折线表示y与x之间的函数关系,根据图象进行以下探究:
首条贯通丝绸之路经济带的高铁线--宝兰客专进入全线拉通试验阶段.宝兰客专的通车对加快西北地区与“一带一路”沿线国家和地区的经贸合作、人文交流具有十分重要的意义.试运行期间,一列动车从西安开往西宁,一列普通列车从西宁开往西安,两车同时出发,设普通列车行驶的时间为x(小时),两车之间的距离为y(千米),图中的折线表示y与x之间的函数关系,根据图象进行以下探究: