题目内容
7.如图,在△ABC中,点A在x轴负半轴上,点B在x轴正半轴上,OB=5,点C在y轴负半轴上,且OC=5,抛物线y=a(x-2)2+k经过△ABC的三个顶点.(1)求抛物线的解析式;
(2)设横坐标为t的点P为抛物线上位于直线BC下方的一点,过点P作PQ∥BC交x轴于点Q,若直线PQ与直线BC之间的距离为d(d≠0),求d与t之间的函数关系式(直接写出自变量的取值范围);
(3)在(2)的条件下,连接PA交BC于点E,当t为何值时,使AE=2PE?

分析 (1)根据题意得出B,C点坐标,直接代入解析式求出即可;
(2)作PN⊥y轴,延长BC交PN于点M,作BR⊥PQ,利用抛物线y=x2-4x-5,得出点B,C的坐标,求出MP的长,在RT△BRQ中∠RBQ=45°,即可得出d与t之间的函数关系式.
(3)由BQ=-t2+5t,AB=6,结合平行线分线段成比例列出式子求解即可得出t的值.
解答 解:(1)∵OB=5,点C在y轴负半轴上,且OC=5,
∴B(5,0),C(0,-5)代入抛物线解析式得:
$\left\{\begin{array}{l}{9a+k=0}\\{-5=4a+k}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=1}\\{k=-9}\end{array}\right.$
∴抛物线y=(x-2)2-9=x2-4x-5;
(2)如图1,作PN⊥y轴,延长BC交PN于点M,作BR⊥PQ,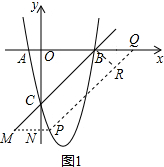
∵抛物线y=x2-4x-5,
∴B(5,0),
∴OC=OB=5,
∴∠OCB=45°,
∴∠MCN=45°,
∴CN=MN,
∵P(t,t2-4t-5),
∴MN=CN=-(t2-4t-5)-5=-t2+4t,
∴MP=MN+NP=-t2+4t+t=-t2+5t
∵四边形MPQB是平行四边形,
∴BQ=-t2+5t,
∵在RT△BRQ中∠RBQ=45°,
∴d=(-t2+4t)×$\frac{\sqrt{2}}{2}$=-$\frac{\sqrt{2}}{2}$t2+2$\sqrt{2}$t.(0<t<5)
(3)如图2,连接AP交BC于点E,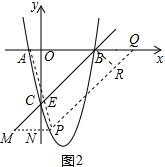
由(2)可知BQ=-t2+5t,
∵AB=6,
∴$\frac{AE}{PE}$=$\frac{AB}{BQ}$,
∵AE=2PE,
∴2=$\frac{6}{-{t}^{2}+5t}$,
解得:t1=$\frac{5-\sqrt{13}}{2}$,t2=$\frac{5+\sqrt{13}}{2}$.
点评 本题主要考查了二次函数与方程、几何知识的综合应用,解题的关键是善于将函数问题转化为方程问题,善于利用几何图形的有关性质、定理和二次函数的知识求解.

 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案 如图,四边形ABCD中,∠BCD=∠D=90°,AD=DC,点E在DC边上,连接BE、EA,EA平分∠BED,点F是BE上一点,AF⊥BE于F,连接CF.
如图,四边形ABCD中,∠BCD=∠D=90°,AD=DC,点E在DC边上,连接BE、EA,EA平分∠BED,点F是BE上一点,AF⊥BE于F,连接CF. 如图,在每个小正方形边长为1的方格纸中,△ABC的顶点都在方格纸格点上.
如图,在每个小正方形边长为1的方格纸中,△ABC的顶点都在方格纸格点上. 如图,在四边形ABCD中,AB=BC,BF是∠ABC的平分线,CA是∠DCF的平分线.求证:AF∥DC.
如图,在四边形ABCD中,AB=BC,BF是∠ABC的平分线,CA是∠DCF的平分线.求证:AF∥DC.