题目内容
17. 如图,四边形ABCD中,∠BCD=∠D=90°,AD=DC,点E在DC边上,连接BE、EA,EA平分∠BED,点F是BE上一点,AF⊥BE于F,连接CF.
如图,四边形ABCD中,∠BCD=∠D=90°,AD=DC,点E在DC边上,连接BE、EA,EA平分∠BED,点F是BE上一点,AF⊥BE于F,连接CF.(1)求证:DE=EF;
(2)若AE∥CF,BF=2,BC=4,求AB长.
分析 (1)利用“AAS”证得△ADE≌△AFE,得出结论即可;
(2)作AG⊥CB,交CB的延长线于G,先证明四边形AGCD是正方形,得出AG=AD=AF,再由HL证明Rt△ABG≌Rt△ABF,得出对应边相等BG=BF,求出AG=CG,然后根据勾股定理求出AB.
解答 (1)证明:∵AF⊥BE,∠BCD=∠D=90°,
∴∠AFE=∠D=90°,
∵EA平分∠BED,
∴∠FEA=∠DEA,
在△ADE和△AFE中,
$\left\{\begin{array}{l}{∠D=∠AFE}\\{∠DEA=∠FEA}\\{AE=AE}\end{array}\right.$,
∴△ADE≌△AFE(AAS),
∴DE=EF;
(2)解:作AG⊥CB,交CB的延长线于G,如图所示: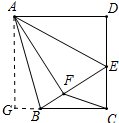 则∠AGC=90°,
则∠AGC=90°,
∵∠BCD=∠D=90°,
∴四边形AGCD是矩形,
∵AD=DC,
∴矩形AGCD是正方形,
∴AG=AD=CG,
∵△ADE≌△AFE,
∴AD=AF,
∴AG=AF,
在Rt△ABG和Rt△ABF中,
$\left\{\begin{array}{l}{AB=AB}\\{AG=AF}\end{array}\right.$,
∴Rt△ABG≌Rt△ABF(HL),
∴BG=BF=2,
∴AG=CG=BC+BG=6,
根据勾股定理得:AB=$\sqrt{A{G}^{2}+B{G}^{2}}$=$\sqrt{{6}^{2}+{2}^{2}}$=2$\sqrt{10}$.
点评 本题考查了全等三角形的判定与性质、正方形的判定与性质、勾股定理的运用;证明三角形全等和正方形是解决问题的关键.

练习册系列答案
 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
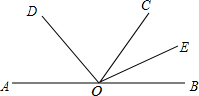 如图,O为直线AB上一点,射线OD、OE分别平分∠AOC、∠BOC,求∠DOE的度数.
如图,O为直线AB上一点,射线OD、OE分别平分∠AOC、∠BOC,求∠DOE的度数.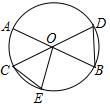 如图,AB、CD为⊙O的直径,$\widehat{AC}$=$\widehat{CE}$,求证:BD=CE.
如图,AB、CD为⊙O的直径,$\widehat{AC}$=$\widehat{CE}$,求证:BD=CE.