题目内容
12. 如图,在每个小正方形边长为1的方格纸中,△ABC的顶点都在方格纸格点上.
如图,在每个小正方形边长为1的方格纸中,△ABC的顶点都在方格纸格点上.(1)△ABC的面积为8;
(2)将△ABC经过平移后得到△A′B′C′,图中标出了点B的对应点B′,补全△A′B′C′;
(3)若连接AA′,BB′,则这两条线段之间的关系是平行且相等;
(4)在图中画出△ABC的高CD;
(5)能使S△ABC=S△QBC的格点Q,共有4个.
分析 (1)根据三角形的面积公式列式计算即可得解;
(2)根据网格结构找出点A′、C′的位置,然后顺次连接即可;
(3)根据平移的性质,对应点的连线互相平行且相等解答;
(4)根据三角形的高线的定义作出即可;
(5)根据等底等高的三角形的面积相等找出即可.
解答 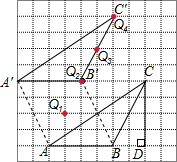 解:(1)△ABC的面积=$\frac{1}{2}$×4×4=8;
解:(1)△ABC的面积=$\frac{1}{2}$×4×4=8;
(2)△A′B′C′如图所示;
(3)AA′与BB′平行且相等;
(4)△ABC的高CD如图所示;
(5)如图,格点Q共有4个.
故答案为:(1)8;(3)平行且相等;(5)4.
点评 本题考查了利用平移变换图形,三角形的面积,等底等高的三角形的面积相等,以及三角形的高线的定义,熟记各性质是解题的关键.

练习册系列答案
 互动英语系列答案
互动英语系列答案
相关题目
17.请你按下列程序进行计算,把答案填写在表格内,然后看看有什么规律,想想为什么会有这样的规律?

(1)填写表内的空格:
(2)你发现的规律是:(n2+n)÷n-n=1.

(1)填写表内的空格:
| 输入 n | 3 | 2 | -2 | $\frac{1}{3}$ | … |
| 输出答案y | 1 | 1 | 1 | 1 | … |
2.已知事件A为必然事件,则概率P(A)的值( )
| A. | 等于0 | B. | 大于1 | C. | 等于1 | D. | 0<P(A)<1 |
