题目内容
20．矩形木板长和宽分别为120厘米和80厘米，在4个角上各剪去边长为x厘米的正方形，则余下的面积S（平方厘米）与x（厘米）之间的函数关系式为S=-4x2+9600，自变量取值范围为0＜x＜40．分析 根据面积的和差，可得函数关系式，根据小正方形的边长之和小于矩形的宽，可得答案．
解答 解：由题意，得
S=-4x2+9600，
由小正方形的边长之和小于矩形的宽，得
2x＜80，且x＞0，
解得0＜x＜40，
故答案为：S=-4x2+9600.0＜x＜40．
点评 本题考查了函数关系式，利用面积的和差是解题关键，注意小正方形的边长要大于零且小于矩形宽的一半．
练习册系列答案
应用题作业本系列答案
相关题目
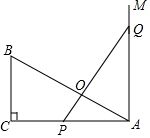如图，已知△ABC是直角三角形，∠C=90°，AC=10cm，BC=5cm，射线AM⊥AC，点P在AC上运动（不与点A，C重合），点Q在AM上运动（不与点A重合），且始终保持PQ=AB．
15．
如图，在△ABC中，∠ACB=90°，AD平分∠BAC，DE⊥AB于点E，则下列结论错误的是（ ）
如图，在△ABC中，∠ACB=90°，AD平分∠BAC，DE⊥AB于点E，则下列结论错误的是（ ）| A． | BD+ED=BC | B． | ED+AC＞AD | C． | DA平分∠EDC | D． | DE平分∠ADB |
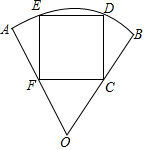要在半径长为1米、圆心角为60°的扇形铁皮（如图）上截取一块面积尽可能大的正方形，请你设计一个截取方案（画出示意图），并计算这个正方形铁皮的面积（精确到0.01）．
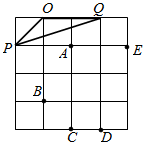如图，△OPQ在边长为1个单位的方格纸中，它们的顶点在小正方形顶点位置，点A，B，C，D，E也是小正方形的顶点，从点A，B，C，D，E中选取三个点所构成的三角形与△OPQ相似，那么这个三角形是△CDB．