题目内容
5.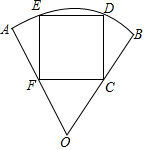 要在半径长为1米、圆心角为60°的扇形铁皮(如图)上截取一块面积尽可能大的正方形,请你设计一个截取方案(画出示意图),并计算这个正方形铁皮的面积(精确到0.01).
要在半径长为1米、圆心角为60°的扇形铁皮(如图)上截取一块面积尽可能大的正方形,请你设计一个截取方案(画出示意图),并计算这个正方形铁皮的面积(精确到0.01).
分析 根据题意画出图形,分别连接PQ和过O作OG⊥DE,交CF于点H,连接OF,构造直角三角形求得正方形的边长,求得正方形的面积后比较即可.由于正方形内接于扇形,故应分两种情况进行讨论.
解答 解:有如下两种截取方式,
方案一:如图1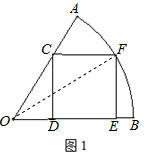
连接OF,设正方形CDEF的边长为x,
∵圆心角为60°,
∴OD=CDcot∠AOB=$\frac{\sqrt{3}}{3}$x,
则在Rt△OFE中,
OF2=OE2+EF2,即12=x2+(x+$\frac{\sqrt{3}}{3}$x)2,
解得x2=$\frac{21-6\sqrt{3}}{37}$,
∴S四边形CDEF=x2=$\frac{21-6\sqrt{3}}{37}$≈0.29;
方案二:如图2所示,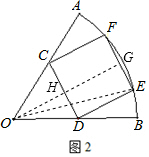
过O作OG⊥EF,交CD于点H,连接OE,
设EG=x,
∵四边形CDEF是正方形,
∴OH⊥CD,
∴EG=DH=x,
∵∠DOC=60°,H为CD中点,
∴OH=$\sqrt{3}$DH,
∴OG=OH+HG=$\sqrt{3}$HC+CF=$\sqrt{3}$x+2x,
在Rt△OEG中,
OE2=GE2+OG2,即12=x2+($\sqrt{3}$x+2x)2,
解得x2=$\frac{2-\sqrt{3}}{4}$,
∴S四边形CDEF=4x2=2-$\sqrt{3}$≈0.27,
∴第(一)种方案截取的正方形的面积最大.
点评 本题考查的是垂径定理及勾股定理,解答此题的关键是根据题意画出图形,作出辅助线,构造出直角三角形,再进行解答.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
10.在△ABC和△DEF中,AB=AC,DE=DF,根据下列条件,能判断△ABC和△DEF相似的是( )
| A. | $\frac{AB}{DE}$=$\frac{AC}{DF}$ | B. | $\frac{AB}{DE}$=$\frac{BC}{EF}$ | C. | ∠A=∠E | D. | ∠B=∠D |
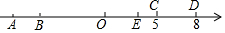 如图,数轴上有A、B、C、D、O五个点,点O为原点,点C在数轴上表示的数是5,线段CD的长度为3个单位,线段AB的长度为1个单位,且B、C两点之间的距离为12个单位,请解答下列问题:
如图,数轴上有A、B、C、D、O五个点,点O为原点,点C在数轴上表示的数是5,线段CD的长度为3个单位,线段AB的长度为1个单位,且B、C两点之间的距离为12个单位,请解答下列问题: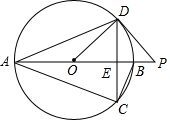 已知:如图,AB是⊙O的直径,CD是弦,且AB⊥CD于E,P是AB延长线上一点,连接PD,∠PDC=∠CAD.
已知:如图,AB是⊙O的直径,CD是弦,且AB⊥CD于E,P是AB延长线上一点,连接PD,∠PDC=∠CAD.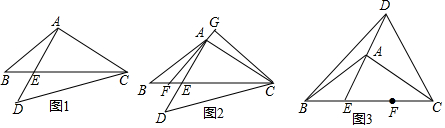
 如图,在直角三角形ABC中,两锐角平分线AM、BN所夹的钝角∠AOB=135度.
如图,在直角三角形ABC中,两锐角平分线AM、BN所夹的钝角∠AOB=135度.