题目内容
12.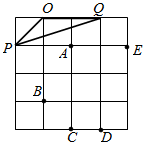 如图,△OPQ在边长为1个单位的方格纸中,它们的顶点在小正方形顶点位置,点A,B,C,D,E也是小正方形的顶点,从点A,B,C,D,E中选取三个点所构成的三角形与△OPQ相似,那么这个三角形是△CDB.
如图,△OPQ在边长为1个单位的方格纸中,它们的顶点在小正方形顶点位置,点A,B,C,D,E也是小正方形的顶点,从点A,B,C,D,E中选取三个点所构成的三角形与△OPQ相似,那么这个三角形是△CDB.
分析 连接BC、BD,由正方形的性质得出∠BCD=∠QOP,由勾股定理得:OP=BC=$\sqrt{2}$,证出$\frac{OP}{CD}=\frac{QO}{BC}=\frac{\sqrt{2}}{1}$,得出△OPQ∽△CDB即可.
解答 解: 与△OPQ相似的是△BCD;理由如下:
与△OPQ相似的是△BCD;理由如下:
连接BC、BD,如图所示:
则∠BCD=90°+45°=135°=∠QOP,
由勾股定理得:OP=BC=$\sqrt{2}$,
∵OQ=2,CD=1,
∴$\frac{OP}{CD}=\frac{QO}{BC}=\frac{\sqrt{2}}{1}$,
∴△OPQ∽△CDB;
故答案为:△CDB.
点评 本题考查了相似三角形的判定定理、正方形的性质以及勾股定理;熟练掌握相似三角形的判定定理和勾股定理是解决问题的关键.

练习册系列答案
相关题目
7.下列说法正确的是( )
| A. | 处于中间位置的数为这组数的中位数 | |
| B. | 中间两个数的平均数为这组数的中位数 | |
| C. | 想要了解一批电磁炉的使用寿命,适合采用全面调查的方法 | |
| D. | 公司员工月收入的众数是3500元,说明该公司月收入为3500元的员工最多 |
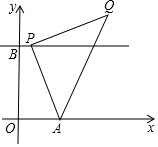 如图,在平面直角坐标系中,A(1,0),B(0,2),过点B作直线l∥x轴,点P(a,2)是直线l上的动点,以AP为边在AP右侧作等腰Rt△APQ,使∠APQ=Rt∠.
如图,在平面直角坐标系中,A(1,0),B(0,2),过点B作直线l∥x轴,点P(a,2)是直线l上的动点,以AP为边在AP右侧作等腰Rt△APQ,使∠APQ=Rt∠.