题目内容
11.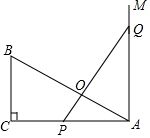 如图,已知△ABC是直角三角形,∠C=90°,AC=10cm,BC=5cm,射线AM⊥AC,点P在AC上运动(不与点A,C重合),点Q在AM上运动(不与点A重合),且始终保持PQ=AB.
如图,已知△ABC是直角三角形,∠C=90°,AC=10cm,BC=5cm,射线AM⊥AC,点P在AC上运动(不与点A,C重合),点Q在AM上运动(不与点A重合),且始终保持PQ=AB.(1)点P在AC上运动到什么位置时,△ABC和△QPA全等?请说明理由.
(2)在(1)的情况下,猜想PQ与AB有什么位置关系,并证明你的结论.
分析 (1)分情况讨论:①Rt△APQ≌Rt△CBA,此时AP=BC=5,可据此求出P点的位置.②Rt△QAP≌Rt△BCA,此时AP=AC,P、C重合,不合题意;
(2)由全等三角形的性质知∠B=∠QPA,又∠B+∠BAC=90°,可得∠QPA+∠BAC=90°,即∠POA=90°,即可得答案.
解答 解:(1)根据三角形全等的判定方法HL可知:
①当P运动到AP=BC时,
∵∠C=∠QAP=90°,
在Rt△ABC与Rt△QPA中,$\left\{\begin{array}{l}{AP=BC}\\{PQ=AB}\end{array}\right.$,
∴Rt△ABC≌Rt△QPA(HL),
即AP=BC=5;
②当P运动到与C点重合时,AP=AC,不合题意.
综上所述,当点P运动到距离点A为5时,△ABC与△APQ全等;
(2)由(1)知,Rt△ABC≌Rt△QPA,
∴∠B=∠QPA,
又∵∠B+∠BAC=90°,
∴∠QPA+∠BAC=90°,即∠POA=90°,
∴PQ⊥AB.
点评 本题考查三角形全等的判定方法和全等三角形的性质,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.由于本题没有说明全等三角形的对应边和对应角,因此要分类讨论,以免漏解.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
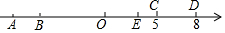 如图,数轴上有A、B、C、D、O五个点,点O为原点,点C在数轴上表示的数是5,线段CD的长度为3个单位,线段AB的长度为1个单位,且B、C两点之间的距离为12个单位,请解答下列问题:
如图,数轴上有A、B、C、D、O五个点,点O为原点,点C在数轴上表示的数是5,线段CD的长度为3个单位,线段AB的长度为1个单位,且B、C两点之间的距离为12个单位,请解答下列问题: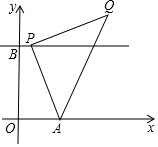 如图,在平面直角坐标系中,A(1,0),B(0,2),过点B作直线l∥x轴,点P(a,2)是直线l上的动点,以AP为边在AP右侧作等腰Rt△APQ,使∠APQ=Rt∠.
如图,在平面直角坐标系中,A(1,0),B(0,2),过点B作直线l∥x轴,点P(a,2)是直线l上的动点,以AP为边在AP右侧作等腰Rt△APQ,使∠APQ=Rt∠.