题目内容
分解因式：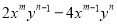 
（m,n均为大于1的整数）
【解析】试题分析：根据m,n均为大于1的整数，确定出指数最小的是哪一项，然后确定公因式再提取公因式即可.
试题解析：
练习册系列答案
相关题目
文文和彬彬在证明“有两个角相等的三角形是等腰三角形”这一命题时，画出图形，写出“已知”，“求证”（如图），她们对各自所作的辅助线描述如下：
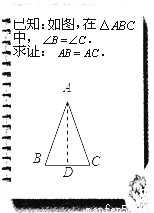
文文：“过点A作BC的中垂线AD，垂足为D”；
彬彬：“作△ABC的角平分线AD”．
数学老师看了两位同学的辅助线作法后，说：“彬彬的作法是正确的，而文文的作法需要订正．”
（1）请你简要说明文文的辅助线作法错在哪里；
（2）根据彬彬的辅助线作法，完成证明过程．
（1）作辅助线不能同时满足两个条件；（2）证明见解析.
【解析】试题分析：（1）线段BC的中垂线可以直接作出的，不需要附带“过点A作”；
（2）根据已知条件利用AAS可证△ABD≌△ACD，得出AB=AC．
试题解析：（1）作辅助线不能同时满足两个条件；
（2）证明：作△ABC的角平分线AD．
∴∠BAD=∠CAD，
在△ABD与△ACD中，
∴△ABD≌... 写出一个解集为x＞1的一元一次不等式：__________．
2x-1＞1（答案不唯一）
【解析】试题分析：【解析】
移项，得x﹣1＞0（答案不唯一）．
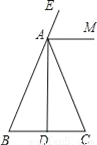
故答案为x﹣1＞0． 如图，在△ABC中，AB=AC，AD是高，AM是△ABC外角∠CAE的平分线．
（1）用尺规作图方法，作∠ADC的平分线DN；（保留作图痕迹，不写作法和证明）
（2）设DN与AM交于点F，判断△ADF的形状．（只写结果）
（1）作图见解析；（2）△ADF是等腰直角三角形.
【解析】试题分析：（1）以D为圆心，以任意长为半径画弧，交AD于G，交DC于H，分别以G、H为圆心，以大于GH为半径画弧，两弧交于N，作射线DN，交AM于F．
（2）求出∠BAD=∠CAD，求出∠FAD=×180°=90°，求出∠CDF=∠AFD=∠ADF，推出AD=AF，即可得出答案．
【解析】
（1）如图所示：
（2... 如图，在△ABC中，AB=AC，E是AB的中点，以点E为圆心，EB为半径画弧，交BC于点D，连接ED并延长到点F，使DF=DE，连接FC，若∠B=70°，则∠F的度数是（ ）
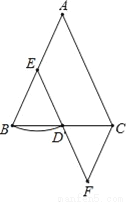
A. 40 B. 70 C. 50 D. 45
A
【解析】【解析】
∵以点E为圆心，EB为半径画弧，交BC于点D，∴EB=ED，∴∠EDB=∠B=70°，∴∠BED=180°﹣∠B=∠BDE=40°．
∵AB=AC，∴∠ACB=∠B，∴∠EDB=∠ACB，∴EF∥AC．
∵E是AB的中点，即BE=AE，∴BD=CD．
在△EBD和△FCD中，∵DE=DF，∠EDB=∠CDF，BD=CD，∴△EBD≌△FCD（SAS）...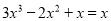 
(______)
【解析】根据提公因式法分解因式，可得=x（）.
故答案为： . 将
分解因式，应提取的公因式是___________
【解析】由x-y与y-x互为相反数，变形后提公因式3（x-y），可得=3（x-y）（a-3b）.
故答案为：3（x-y）. 如果x2+2(m-3)x+25能用公式法分解因式，那么m的值是多少？
m=8或-2．
【解析】试题分析：利用完全平方公式的结构特征判断即可确定出m的值，注意包括两种情况．
试题解析：∵x2+2（m-3）x+25能用公式法分解因式，
∴2（m-3）=±10，
解得：m=8或-2． 如图，在△ABD中，AC⊥BD，点C是BD的中点，则下列结论错误的是（ ）
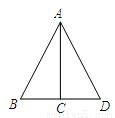
A. AB=AD B. AB=BD C. ∠B=∠D D. AC平分∠BAD
B
【解析】∵AC⊥BD，点C是BD的中点，
∴AB=AD（线段中垂线的性质）
∴∠B=∠D（等边对等角）
∴∠BAC=∠DAC（等腰三角形三线合一）
∴AC平分∠BAD，
故选：B .